Потенциална точност на измерване, страница 2
методи за обработка на резултатите от измерванията и оценка на показателите за точност на измерванията;
изисквания към квалификацията на операторите;
изисквания за безопасност.
В сертификатите за методи за измерванепосочете:
цел и обхват на методиката;
типове и брой екземпляри на средствата за измерване, използвани за измервания. Номерът на екземпляр на измервателен уред в сертификата не е посочен, ако стойностите на показателите за точност на измерване, посочени в сертификата, са определени, като се вземе предвид възможността за използване на всеки екземпляр на измервателен уред от този тип;
технически характеристики на спомагателните устройства, необходими за извършване на измервания;
процедурата за подготовка и извършване на измервания;
числени стойности на показателите за точност на измерване;
интервали на калибриране на средствата за измерване и набор от нормативни документи, съгласно които трябва да се извърши тяхната проверка;
изисквания към квалификацията на операторите;
изисквания за безопасност.
Точността на измерване зависи до голяма степен и от алгоритъма за обработка на експерименталните данни. Това е причината за изискванетосертифициране на алгоритми.
В някои области и видове измервания, със съвременна стандартна база, е постигната точност, която прави възможно извършването на измервания намолекулярно ниво.Формално отражение на това е появата на константата на Болцманk=1,38 • 10 -23 J / K в изрази, описващи влияещите фактори, които трябва да бъдат взети предвид. Частиците на материята - атоми, молекули, както и електрическите заряди извършват непрекъснати хаотични движения, чийто интегрален интензитет се характеризира стермодинамична температура T. Колкото по-интензивни са движенията, нареченифлуктуации,толкова по-висока е абсолютната температура T. Флуктуациите създаватшумов ефект,ограничаващ точността на измерване на физическите величини. Силата на шума на RH се определя от уравнението на Найкуист:
,
където f е честотната лента на инструмента. Понякога този израз се допълва от спектралния коефициент N, който отчита ефекта на изстрела в електронни устройства и други явления.
.
Вместо RS мощност, можем да разгледаме шумовата енергия GS и
Ако изхождаме от факта, че енергията на полезния сигнал Р ×t,където Р е мощността, аt —времето за измерване, трябва да бъде по-голяма от енергията на шума, тогава възможността за извършване на измервания на молекулярно ниво ще бъде ограничена от изискването за изпълнение на неравенството
P ×tGSH.
Използвайки разликите в статистическата природа на шума и полезните сигнали, в много случаи е възможно да се преодолеят ограниченията, наложени от законите на термодинамиката. По-специално, некохерентността на шума прави възможно с многократно измерване, натрупване, оптимално филтриране и чрез използването на други техники да се гарантира изпълнението
измервания при отношение .
Основните ограничения на следващото ниво се дължат на дискретността на измерените величини (невъзможно е например да се измери заряд, по-малък от заряда на електрона) или флуктуации, определени от дискретността на материята и енергията. Точността на измерване на това ниво е ограничена от законите на квантовата механика.
Формално отражение на достигането наквантово-механичното ниво на точност на измерванее появата в математическото описание на фактори, които не могат да бъдат пренебрегнати, константата на Планкh= 6.63 • 10 - 34 J/Hz. Един от тези фактори епринципътНесигурността на Хайзенберг,свързваща (чрез константата на Планк) точността на измерване на позицията и импулса на частица, време и енергия, както и други двойки физически величини. Точността на измерване при такива условия става въпрос на разумен компромис.
8.2. ОПРЕДЕЛЯНЕ НА ТОЧНОСТТА НА ИЗМЕРВАНИЯТА ЧРЕЗ ИЗЧИСЛЕНИЕ
Потенциалната точност на измерванията, определена на всяко ниво на развитие на науката и технологиите от точността на държавните стандарти, е недостижима в ежедневието. Ето защо естествено възниква въпросът за реално постижимата точност на измерване. Когато решават този проблем, те винаги изхождат от анализа на конкретен проблем с измерването и се опитват да вземат предвид всички възможни ограничения възможно най-пълно.
Да предположим, че е известно предварително, че сигналътX(t)на изхода на линеен измервателен преобразувател с коефициент на преобразуване, равен на 1, ще бъде смес от полезния сигнал X(t) = Q = const и шумова интерференцияN(t)под формата на нормален стационарен случаен процес със средна стойност, равна на нула, поради външни и вътрешни влияещи фактори. Възможни са следните начини за измерване на неизвестната стойност на Q:
осредняванеХ (t)във времето (по време на едно изпълнение);
осредняване наX (t)върху набор от стойности, свързани във всяка реализация към една и съща точка във времето;
осреднявайкиХ (t)както за множеството, така и за времето. Заедно с това метрологичното осигуряване на измерванията може да се организира по различни начини. В една от опциите (виж фиг. 161, а) информацията за размера на единицата се предава само на измервателния преобразувател. В този случай сигналът на изхода на измервателния преобразувател
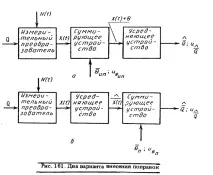
могат да бъдат изменени. Точната му стойност обикновено е неизвестна, което се взема предвидситуационен модел за корекция. След това усредняващото устройство извършва необходимите математически операции.
Във втория вариант информацията за размера на единицата се предава на измервателното устройство като цяло, включително както измервателния преобразувател, така и усредняващото устройство. В този случай корекцията се прави при необходимост в показанието на уреда - фиг. 161,b.
Аналог на стандартното отклонение на резултата от измерването.Изразите за него са дадени в табл. 50, където е дисперсията на шумовите смущения;
—аналог на стандартното отклонение в модела за ситуационна корекция; е интервалът на корелация на нормален стационарен случаен процесХ(t);TP е продължителността на изпълнение на същия процес;n —номер на реализация. При съставянето на табл. 50 се взема предвид, че в първия вариант корекцията се въвежда в моментните стойностиX(t)счрез последващо цифрово осредняване на резултантния масив. Корекцията за неточността на дискретното осредняване има дисперсия.

Раздел. 50 ви позволява да анализирате зависимостта на точността на измерване от много фактори. Така, например, зависимостта на точността от количеството експериментални данни(n,Tr) е очевидна. Ограничаването на количеството експериментални данни ограничава точността на измерванията. Може да се види зависимостта на точността от дизайна и схемните решения (метод на осредняване, стойност). Има възможност за алтернативен избор, а при ограничения в избора - директно изчисляване на точността на измерване. Два варианта представят подходи за метрологична поддръжка, чието качество се определя от стойностите и . Зависимостта на точността от априори
информация за влияещи фактори(,).Ако е точнаняма информация за параметрите на смущението, а е известен само законът за разпределение на тяхната вероятност
Когатоp(,) =p()p()този двоен интеграл е лесен за изчисляване във всеки отделен случай.
Според таблицата 50 във всеки конкретен случай е лесно да се намери минималната стойност,т.е. определяне на максималната възможна точност при избраните условия и ограничения.
По същия начин, точността на измерванията се изчислява и анализира в по-сложни случаи, които се различават по това, че трябва да се вземат предвид повече фактори.
- AltGTU 419
- AltGU 113
- AMPGU 296
- ASTU 266
- BITTU 794
- BSTU "Voenmekh" 1191
- BSMU 172
- BSTU 602
- BSU 153
- BSUIR 391
- БелГУТ 4908
- BSEU 962
- БНТУ 1070
- BTEU PK 689
- БрСУ 179
- ВНТУ 119
- VGUES 426
- ВлГУ 645
- VMEDA 611
- ВолгГТУ 235
- ВНУ им. Далия 166
- VZFEI 245
- ВятГША 101
- ВятГГУ 139
- ВятГУ 559
- GGDSK 171
- GomGMK 501
- GSMU 1967
- GSTU im. Сухой 4467
- ГСУ им. Скарина 1590г
- GMA им. Макарова 300
- ГДПУ 159
- DalGAU 279
- DVGGU 134
- DVGMU 409
- DVGTU 936
- DVGUPS 305
- FEFU 949
- ДонГТУ 497
- DITM MNTU 109
- IVGMA 488
- IGHTU 130
- ИжГТУ 143
- KemGPPC 171
- KemGU 507
- KSMTU 269
- Киров АТ 147
- KGKSEP 407
- KGTA им. Дегтярев 174
- КнАГТУ 2909
- КрасГАУ 370
- КрасГМУ 630
- KSPU им. Астафиева 133
- KSTU (SFU) 567
- КГТЕИ (СФУ) 112
- PDA № 2 177
- КубГТУ139
- КубСУ 107
- KuzGPA 182
- КузГТУ 789
- MSTU им. Носова 367
- МГУ ги. Сахарова 232
- IPEC 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- MGIU 1179
- MGOU 121
- MGSU 330
- Московски държавен университет 273
- МГУКИ 101
- MGUPI 225
- MGUPS (MIIT) 636
- МГУТУ 122
- MTUCI 179
- ХАЙ 656
- TPU 454
- NRU MPEI 641
- НМСУ "Горни" 1701
- ХПИ 1534
- НТУУ "КПИ" 212
- НУК тях. Макарова 542
- HB 777
- NGAVT 362
- NSAU 411
- NGASU 817
- NGMU 665
- NGPU 214
- NSTU 4610
- НГУ 1992г
- NSUE 499
- NII 201
- OmGTU 301
- OmGUPS 230
- СПбПК №4 115
- PGUPS 2489
- ПСПУ им. Короленко 296
- ПНТУ им. Кондратюк 119
- RANEPA 186
- ROAT MIIT 608
- RTA 243
- RSHU 118
- РГПУ им. Херцен 124
- РГППУ 142
- RSSU 162
- "МАТИ" - РГТУ 121
- РГУНиГ 260
- REU ги. Плеханов 122
- РГАТУ им. Соловьова 219
- RyazGMU 125
- RGRTU 666
- SamGTU 130
- СПбГАСУ 318
- INGECON 328
- СПбГИПСР 136
- СПбГЛТУ им. Киров 227
- СПбГМТУ 143
- СПбГПМУ 147
- SPbGPU 1598
- СПбГТИ (ТУ) 292
- СПбГТУРП 235
- Държавен университет в Санкт Петербург 582
- GUAP 524
- СПбГУНИПТ 291
- СПбГУПТД 438
- СПбГУСЕ 226
- СПбГУТ 193
- СПГУТД 151
- SPbGUEF 145
- Електротехнически университет в Санкт Петербург "LETI" 380
- ПИМаш 247
- NRU ITMO 531
- СГТУ им. Гагарина 114
- СахСУ 278
- SZTU 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1655 г
- СибГТУ 946
- SGUPS 1513
- СибГУТИ 2083
- СибУПК 377
- SFU 2423
- SNAU 567
- SSU 768
- TRTU 149
- ТОГУ 551
- TGEU 325
- TSU (Томск) 276
- TSPU 181
- ТулГУ 553
- УкрГАЖТ 234
- UlGTU 536
- UIPCPRO 123
- USPU 195
- USTU-UPI 758
- UGNTU 570
- USTU 134
- ХГАЕП 138
- KhSAFC 110
- HNAGH 407
- HNUVD 512
- KhNU им. Каразина 305
- ХНУРЕ 324
- KhNEU 495
- Процесор 157
- ЧитГУ 220
- SUSU 306
За да отпечатате файла, изтеглете го (във формат Word).