Практическо занятие № 2 Определяне на ентропия и обем информация
Определете ентропията на пълна многостепенна йерархична система, чийто брой елементи на всяко ниво се определя отin=kn, n е номерът на нивото, k е основата на системата. Коренът на графиката е на ниво нула.
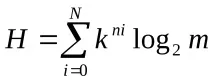
Определете ентропията на изображението на телевизионен приемник, ако той има брой градации от 8500 реда, 700 елемента на ред.
Ако градациите на яркостта са еднакво вероятни и взаимно независими:
Определете количеството информация в думата "пролетар":
а) ако думата е в кода на Бодо
б) ако думата е в стандартния код №3.
P
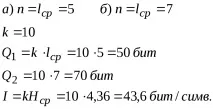
Определете количеството информация при прехвърляне на документ, който съдържа 20 реда текстова и цифрова информация, ако прехвърлянето се извършва с помощта на стандартен код № 3 и всеки ред съдържа 30 знака (включително интервали).
Какво е количеството информация при получаване на 8 съобщения от единен троичен четирицифрен код.
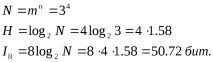
Практически урок № 3 Изчисляване на загубите на информация при предаване на съобщения по комуникационни канали с шум
Определете средното количество информация, съдържаща се в получения ансамбъл от съобщения спрямо основната азбука, ако съобщението е съставено от азбуката A, B, C. В този случай вероятността за появата на букви от азбуката на изхода на източника на съобщението: P(Ai)=P(Bi)=0,25; Р(Сi)=0.5=(вj/ai). Условните вероятности за срещане на двойки от азбуката на форматаinj/аiизглеждат така:
Р(А/А)=0.97, Р(В/А)=0.015, Р(С/А)=0.015 (Св. I)
Р(А/В)=0.02, Р(В/В)=0.97, Р(С/В)=0.01 (II стадий)
Р(А/С)=0.01, Р(В/С)=0.01, Р(С/С)=0.98 (Св. III)
Намираме безусловните вероятности за съвместно появяване на символи от азбуката исъбития:

P


Определяме вероятността за появата на A, B, C от страната на приемника:
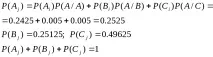
Средното количество информация в ансамбъла от получени съобщения се изразява по формулата:
От таблицата намираме:
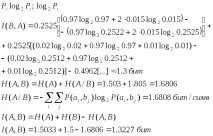
2. Съобщението на българската азбука се предава в петцифрен код Бодо с помощта на стандартен телеграф. Писмата се предават с пет елементарни пакета с 1=20ms – време за предаване, 2=30ms – начало, 3=45ms – стоп. Определете: а) каква е скоростта на предаване на информацията, б) каква е скоростта на предаване на всеки и
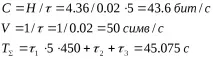
3

Изчисляваме съвместните вероятности и ги поставяме в таблицата:

Дефинираме безусловна и условна ентропия:
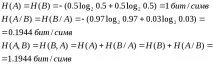
Нека дефинираме пропускателната способност:
Практика #4 Излишък на съобщения
Намерете излишъка на азбуката.

Вероятността за появата на букви от основната азбука на изхода на източника на съобщението:
O
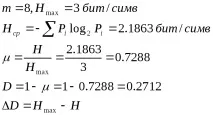
Определете общия и частен излишък на определена 8-буквена азбука, ако е известно, че нейната ентропия е 2,7 бита / символ с взаимно независими иравновероятни символи, а отчитайки тяхната взаимозависимост е по-малко с Н=0,25 бита/символ.

4. Определете излишъка от български текстове за случаите:
а) с равновероятна поява на букви в текста;
б) с неравномерно появяване на буквите в текста;
в) отчитане на двубуквените комбинации;
г) като се вземат предвид трибуквените комбинации.
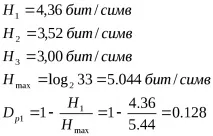
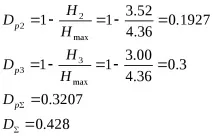
Правило: Излишъкът на съобщенията при кодиране блок по блок на азбучни знаци е по-малък, отколкото в случай на кодиране буква по буква.
Ако цифровото съобщение е кодирано в двоичен код, тогава с блоково кодиране има, така да се каже, увеличение на първичната азбука, т.е. вероятностите на знаците на първичната азбука се изравняват и тяхната ентропия се увеличава, а с това и общата ентропия на азбуката, т.е. натоварването на един знак се увеличава и съответно излишъкът намалява.
При кодиране буква по буква основната азбука изглежда така:
…
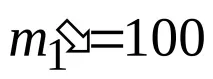
С
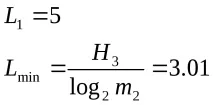
Горната и долната граница на средната дължина на кодовите блокове се определят от неравенството:
M е броят на буквите в блока.
Правило: когато се анализира съотношението на 0 и 1 в двоичен код, може да се види, че колкото по-малко е кодираното число, толкова по-голяма е разликата между 0 и 1 (в полза на 0) в кодовата дума. По този начин излишъкът вече е вграден в двоичния код, той ще намалее с увеличаване на броя на кодовите комбинации M. Средната дължина на кодовата комбинация на двоичния код ще изрази точно необходимия брой двоични знаци само ако вероятностите за поява 0 и 1 саса равни и N е цяло число на 2.