Правила за логаритъм и потенциране
Логаритмична функция
Функция от форматаy =, където a е дадено число, a> 0 и ≠ 0, се наричалогаритмично.
y y
0 х 0 х
a> 1 y =0 0 g(x) > 0
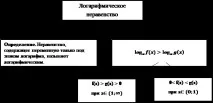
Запомнихте и повторихте теорията! А сега малко отклонение.
Началото на ХХ век. Франция. Париж. Минавайки през площад Екзюпери, мосю Команьон посочи къщата на Денизо: „Нещо вече не се чува за гледача, който общува със светците. Бях заведен там от Лакарел, началник на кабинета на префекта. Тя седеше на стол със затворени очи и около десет почитатели задаваха въпроси ... Тя отговори на всички въпроси в поетичен стил и без много затруднения. Когато редът дойде при мен, зададох най-простия въпрос: "Колко е логаритъмът от 9?". Тя не ми отговори. Как така? Гледачът не знае логаритъма от 9? Това минало ли е! Всички бяха объркани. Тръгнах си, придружена от всеобщо неодобрение.
Доскоро беше трудно да си представим инженер без плъзгаща се линейка в джоба си, изобретена десет години след появата на логаритмите на Нейпиер от английския математикГюнтер.Тя ви позволява бързо да получите отговор, замени микрокалкулатора от инженерна употреба, но нито първите компютри, нито калкулаторите биха били построени без логаритмична линейка.

Звезди, шум и логаритми.
Това заглавие свързва такива на пръв поглед несвързани неща. Шумът и звездите са комбинирани тук, защото силата на шума и яркостта на звездите се оценяват по един и същи начин - в логаритмична скала. Астрономите разделят звездите според степента на яркост на видими и абсолютни звездни величини - звезди от първа величина, втора, трета и т.н. Последователността на видимите звездни величини, възприемани от окото, е аритметикапрогресия. Но физически според друг закон: яркостта на звездите е геометрична прогресия със знаменател 2,5. Лесно е да се разбере, че "величината" на една звезда е логаритъмът на нейната физическа яркост. Накратко, когато оценява яркостта на звездите, астрономът използва таблица с логаритми, базирана на 2,5. Силата на шума се оценява по подобен начин. Вредното влияние на производствения шум върху здравето на работниците и върху производителността на труда доведе до разработването на методи за точна числена оценка на силата на шума. Единицата за сила на звука е "бел", но на практика се използва единицата за сила на звука, равна на неговата десета, така наречените "децибели". Последователни степени на силата на звука 1 бела, 2 бела, 3 бела и т.н. Те образуват аритметична прогресия ... Физическите величини, които характеризират шума (енергия, интензитет на звука и т.н.), съставляват геометрична прогресия със знаменател 10. Силата на звука, изразена в белове, е равна на десетичния логаритъм на съответната физическа величина.
Логаритми и усещания
Усещанията, възприемани от човешките сетива, могат да бъдат причинени от стимули, които се различават един от друг много милиони и дори милиарди пъти. Ударите с чук върху хлъзгава плоча са сто пъти по-силни от тихото шумолене на листата, а яркостта на волтовата дъга е трилиони пъти по-ярка от яркостта на някоя слаба звезда, едва видима в нощното небе. Но никакви физиологични процеси не позволяват да се даде такава гама от усещания. Експериментите показват, че организмът като че ли „логаритмува“ дразненията, които получава, т.е. големината на усещането е приблизително пропорционална на десетичния логаритъм от величината на стимула. Както можете да видите, логаритмите нахлуват и в областта на психологията.
Логаритмична спирала.
Тъй като това уравнение е свързано с логаритмичната функция, тогаваспиралата, изчислена по тази формула, се нарича логаритмична. Живите същества обикновено растат, запазвайки общите очертания на формата си. В същото време те растат във всички посоки - едно възрастно същество е едновременно по-високо и по-дебело от малкото. Но черупките на морските животни могат да растат само в една посока. За да не се разтягат твърде много по дължина, те трябва да се усукват и всеки следващ завой е подобен на предишния. И такъв растеж може да се случи само по логаритмична спирала или някои от нейните пространствени аналози. Затова черупките на много мекотели, охлюви, както и рогата на бозайници като архари (планински кози), са усукани в логаритмична спирала. Можем да кажем, че тази спирала е математически символ на съотношението на формите на растеж. Великият немски поет Йохан Волфганг Гьоте дори го е смятал за математически символ на живота и духовното развитие. Очертанията, изразени с логаритмична спирала, имат не само черупки, но и нишки около центъра в логаритмична спирала. Много галактики също са усукани в логаритмични спирали, по-специално Галактиката, към която принадлежи Слънчевата система.
Защо има нужда от логаритми?
Какво научихте за логаритмите и техните приложения?
Кой от учените, допринесли за развитието на логаритмите, си спомняте?
Какво трябва да се има предвид при решаване на различни задачи с логаритми?