Правила за трансформиране на симплекс таблица
Симплексен метод на таблица
За да се опрости процеса на решаване, първоначалните данни на проблем с линейно програмиране при решаването му по симплексния метод се записват в специални симплексни таблици. Следователно, една от модификациите на симплексния метод се наричатабуличен симплексен метод.Задача за линейно програмиране в канонична форма:
Таблицата източник за задачата изглежда така:
| x1 | x2 | . | xn-1 | xn | b | |
| Е | -a0,1 | -a0,2 | . | -a0,n-1 | -a0,n | -b0 |
| xn+1 | a1,1 | a1,2 | . | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | а2,2 | . | a2,n-1 | a2,n | b2 |
| . | . | . | . | . | . | . |
| xn+m | сутринта, 1 | сутринта, 2 | . | съм, n-1 | съм, н | bm |
x1, x2, xn - начални променливи, xn+1, xn+2, xn+m - допълнителни променливи. Приехме всички допълнителни променливи катоосновни, а началните променливи катонеосновни(допълнителните променливи се записват в първата колона на симплексната таблица, а началните в първия ред). При всяка итерация елементите на симплексната таблица се преизчисляват по определени правила.
Алгоритъм на симплексния метод.
Подготвителен етап
Намаляване на проблема LP до канонична форма
Ако е необходимо да се намери минимум в първоначалната задача, знаците на коефициентите на целевата функция F се обръщат a0,n=-a0,n. Коефициентни знациограничаващите условия със знака "≥" също са обърнати. Ако условието съдържа знака "≤" - коефициентите ще бъдат записани без промени.
Стъпка 0. Компилирайте симплексна таблица, съответстваща на оригиналния проблем
| x1 | x2 | . | xn-1 | xn | b | |
| Е | -a0,1 | -a0,2 | . | -a0,n-1 | -a0,n | -b0 |
| xn+1 | a1,1 | a1,2 | . | a1,n-1 | a1,n | b1 |
| xn+2 | a2,1 | а2,2 | . | a2,n-1 | a2,n | b2 |
| . | . | . | . | . | . | . |
| xn+m | сутринта, 1 | сутринта, 2 | . | съм, n-1 | съм, н | bm |
Стъпка 1. Тест за валидиране.
Проверяваме елементите на колона b (свободни членове) за положителност, ако сред тях няма отрицателни, тогава се намира възможно решение (решението, съответстващо на един от върховете на полиедъра на условията) и преминаваме къмстъпка 2.Ако има отрицателни елементи в колоната със свободни членове, тогава избираме сред тях максималното модулно - задава водещия ред k. В този ред намираме и максималния отрицателен елемент ak,l в модул - той задава водещата колона - l и еводещият елемент.Променливата, съответстваща на водещия ред, се изключва от основата, променливата, съответстваща на водещата колона, се включва в основата. Преизчисляваме симплексната таблица според правилата.
Ако сред свободните членове има отрицателни елементи - и в съответния ред - няма такива, тогава условията на проблема са непоследователни и решениятатя няма.
Ако след преизчисляване в колоната на безплатните членове останат отрицателни елементи, преминете към първата стъпка, ако няма такива, преминете към втората.
Стъпка 2. Тествайте за оптималност.
На предишния етап беше намерено осъществимо решение. Нека го проверим за оптималност. Ако няма отрицателни елементи от симплексната таблица, разположени в ред F (без да се вземе предвид елементът b0 - текущата стойност на целевата функция), тогава се намира оптималното решение.
Ако има отрицателни елементи в ред F, тогава решението трябва да се подобри. Избираме сред отрицателните елементи на реда F максималния модул (с изключение на стойността на функцията b0)
l - колоната, в която се намира, ще бъде водеща. За да намерим водещия ред, намираме съотношението на съответния свободен член и елемента от водещия стълб, при условие че те са неотрицателни.
k - низ, за който това отношение е минимално - водещ. Елемент ak,l - водещ (разрешаващ). Променливата, съответстваща на водещия ред (xk), се изключва от основата, променливата, съответстваща на водещата колона (xl), се включва в основата.
Преизчисляваме симплексната таблица с помощта на формули. Ако има отрицателни елементи в новата таблица след преизчисляване в ред F, преминете къмстъпка 2
Ако е невъзможно да се намери водещият ред, тъй като няма положителни елементи във водещата колона, тогава функцията не е ограничена в областта на възможните решения на проблема - алгоритъмът се прекратява.
Ако в реда F и в колоната със свободни членове всички елементи са положителни, тогава оптималното решение е намерено.
Правила за симплексни трансформации на таблици.
При съставянето на нова симплексна таблица в нея настъпват следните промени:
- Вместо основната променлива xk пишем xl; вместонеосновна променлива xl пишем xk.
- водещият елемент се заменя с реципрочната стойност на ak,l'= 1/ak,l
- всички елементи на водещата колона (с изключение на ak,l) се умножават по -1/ak,l
- всички елементи на водещия ред (с изключение на ak,l) се умножават по 1/ak,l
- останалите елементи на симплексната таблица се трансформират съгласно формулатаai,j'= ai,j- ai,lx ak,j/ ak,l
Схемата за трансформиране на елементите на симплексна таблица (с изключение на водещия ред и водещата колона) се нарича схема "правоъгълник".
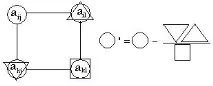
Трансформираният елементai,jи трите съответстващи му фактора са именно върховете на „правоъгълника“.