Принципът на параметричното усилване
Добър пример за обмен на енергия между източник на сигнал и енергоемък параметричен елемент е добре познатият модел с механично разделяне на плочите на зареден кондензатор. За разстилане на плочите, т.е. За да се намали капацитетът, е необходимо да се извърши работа, която увеличава енергийния резерв на кондензатора. Когато плочите се приближат, напротив, част от енергията на полето на кондензатора се преобразува в механична енергия.
Нека разгледаме случая на рязка промяна на капацитета, включен в висококачествена осцилаторна верига, използвайки управляващо напрежение (фиг. 2, а)
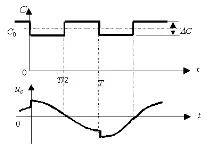
Веригата се влияе от сигналаe(t)=Emcos wt. В този случай честотата на сигнала съвпада с резонансната честота на веригата при средна стойност на капацитета. Скоростта на промяна на капацитета е два пъти по-голяма от честотата на сигнала. Фигура 2b показва напрежението върху капацитета. Фазата на изменение на капацитета е избрана по такъв начин, че капацитетът да намалява в моментите на преходС(t)през максимумите, а увеличението да става в моментите на преминаване през нулата. В моментите, когато капацитетът пада, напрежениетоuc(t)получава увеличение, тъй като зарядът на кондензатора не може да се промени мигновено. Това означава, че енергията на електрическото поле в кондензатора периодично се увеличава и това е еквивалентно на увеличаване на средната мощност на сигнала.
Ако увеличението на енергията поради един скок (надолу) на капацитетаC(t),не превишава консумацията на енергия за времетоT, тогава параметричната верига е стабилна, в противен случай възниква параметрично възбуждане на трептенията. По този начин, чрез регулиране на относителната стойност на DC/C0, т.е. дълбочината на модулация на параметъраC, може да се извърши както параметрично усилване, така и параметрично генериране.
Технически не се извършва рязка промяна на капацитета, а промяна по хармоничен закон със съответната фаза. Това напрежение се подава от генератора на помпата.
Ако амплитудата на сигнала е избрана да бъде много по-малка от амплитудата на помпата, тогава промяната в капацитета под действието на сигнала може да бъде пренебрегната и може да се приеме, че законът за промяна на капацитета се определя само от едно управляващо напрежение. В такъв случай
където , g - начална фаза.
Общият ток през капацитета се определя като
Тъй като честотният компонент на тока не попада в обхвата на прозрачност на веригата, токът във веригата източник на сигнал е сумата от два тока: при честота w и при комбинирана честота, близка до w. Първият от тези токове, изместен по фаза спрямо сигналаe(t)под ъгъл 90 0 , не може да създаде активна проводимост - нито положителна, нито отрицателна. От гледна точка на получаване на ефекта на усилване представлява интерес Рамановото трептене на диференциалната честота, особено в случая, когато . Амплитудата на този ток е В този случай мощността, отделяна от източника на сигнала, се определя като
къдетоGeq- еквивалентна активна проводимост, като се вземе предвид консумацията на енергия от източника на сигнал.
Фигура 3 илюстрира три характерни режима на работа на параметрична верига с променлив капацитет.
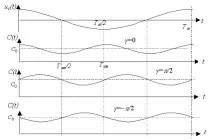
В първия случай (g =0), промяната в енергийния резерв в резервоара за периода е нула, докатоGeq=0. В случая има максимално увеличениеС(t), когато сигналът преминава през максимумите, докато част от енергията, съхранявана в капацитета, отива в устройството, което променя капацитета. По отношение на източника на сигнала това е еквивалентно на шунтиране на постоянния капацитетС0с положителна активна проводимост, в третия случай, когато , активна проводимосте отрицателна, т.е. . Отрицателната активна проводимост отчита притока на енергия от помпения генератор във веригата, съдържащаС(t).
Подобни резултати могат да бъдат получени за периодично променяща се индуктивност.