Разпределителни решетки, ръчна математика

Разпределителни решетки

Определение

Решетката се нарича разпределителна, ако е в сила един от следните закони:

Еквивалентност на два закона за дистрибутивност

Нека е вярно това, тогава добавете от двете страни:

Тук сме използвали един от законите за поглъщане. Сега нека заместим в оригиналния закон за разпределение вместо:

Сравнявайки последните редове в тези две изчисления (във второто използвахме различен закон за абсорбция), заключаваме, че

По подобен начин (променяйки се на и обратно), получаваме доказателство, че полученият закон за разпределение може да се използва за извеждане на оригиналния, използвайки законите за абсорбция, асоциативност и комутативност на операциите.

Примери за разпределителни решетки

Най-простият пример са различните подрешетки на решетката на всички подмножества на определено множество, по-специално решетките на отворени и затворени множества на произволно топологично пространство, двойствено едно към друго (изоморфизъм на двойствеността - приемане на допълнението към цялото пространство).

Пример за неразпределителна решетка

Разгледайте следната диаграма на Хасе:

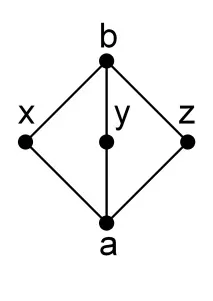
Очевидно е, че тази диаграма дефинира решетка и че , и . Всъщност повечето наистина интересни решетки не са разпределителни.

Неравенство на разпределението

Законът за дистрибутивност под формата на равенство е изпълнен, най-общо казано, не във всички решетки. Въпреки това, може да се види, че в произволна решетка , и следователно . Освен това, което означава. Това означава, че в произволна решетка е валидно следното неравенство:

---