РЕАКТИВНОСТ
1.6. Реактивно съпротивление.
Ако през намотката на индуктор с магнитна верига (ядро) премине променлив ток, променящ се според синусоидалния закон simt (виж фиг. 3), ще има, както казахме, магнитен поток, който магнетизира магнитната верига. Токът и магнитният поток в магнитната верига също ще бъдат променливи и ще възбуждат индукционна ЕМП в намотката. То е равно на напрежението на клемите на намотката и в същото време е пропорционално на скоростта на промяна на магнитния поток. В резултат на това напрежението ще бъде фазово изместено с -90 ° спрямо тока. Това означава, че токът е 90° извън фазата спрямо напрежението. Токът, протичащ през бобината, се нарича реактивен и за разлика от тока през активното съпротивление, той не води до консумация на енергия. В допълнение, напрежението в бобината при фиксиран ток е пропорционално на честотата, следователно съпротивлението на бобината се увеличава с честотата. Напрежението на намотката може да се изчисли съгласно закона на Ом, в който индуктивното съпротивление на намотката трябва да бъде заменено като съпротивление: XL = jL = j2fL(индуктивно съпротивление). Преди обозначението на реактивното съпротивление се поставя символът j, който в математиката означава въображаема стойност, равна на корен квадратен от -1. Сега нека видим какво се случва, ако към пластините на кондензатора се приложи променливо напрежение, което се променя според синусоидалния закон simt. През кондензатора ще тече променлив ток, поради факта, че плочите на кондензатора ще трябва да се зареждат толкова пъти в секунда, колкото пъти токът променя посоката си. Зарядът върху плочите е право пропорционален на приложеното напрежение (q = CU), а токът е пропорционален на скоростта на промяна на заряда (I = dq/dt). По този начин токът през кондензатора също е реактивен, но води пред напрежението с 90°. Текущпропорционално на честотата, следователно капацитетът на кондензатора е обратно пропорционален на честотата: Xc \u003d 1 / jC \u003d -j / C(капацитет). Реактивните съпротивления спрямо честотата са показани на фиг. 6, а. В реалните електрически вериги има както реактивни, индуктивни и капацитивни, така и активни съпротивления. Заедно те образуват комплекс или импеданси, обозначени с буквата Z и математически представляващи комплексни числа, съдържащи реални R и въображаеми X части: Z = R + jX(импеданс).
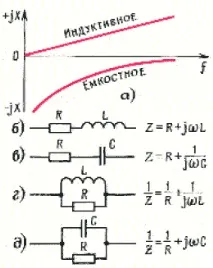
Вече проучихме как се добавят активни съпротивления при последователно и паралелно свързване (фиг. 2, d), а сега остава да кажем, че общите съпротивления се събират по същия начин, просто не забравяйте за знака на реактивното съпротивление и символа j. Ще бъде много полезно, ако тренирате малко и се опитате да напишете импеданса на вериги, съдържащи индуктори, кондензатори и резистори, свързани по различни начини (фиг. 6, b-e). Много скоро ще видите, че един и същ импеданс при една и съща зададена честота може да има вериги, направени по различен начин, и това отваря възможността за преобразуването им. Например верига от резистор и кондензатор, свързани последователно, може да бъде заменена от верига, в която същите елементи са свързани паралелно, но, разбира се, техните номинални стойности ще бъдат различни. Също така е лесно да се види, че когато две бобини са свързани последователно, техните индуктивности се сумират, но капацитетите се сумират, когато кондензаторите са свързани паралелно. Е, сега да преминем към обещаната история за трансформаторите.