Решение Каква трябва да бъде максималната дължина на изпъкнал симетричен по отношение на
Задачата:
Каква трябва да е максималната дължина на изпъкнал, вертикално симетричен мост с радиус 100 m, за да може по него да премине автомобил със скорост 90 km/h, без да напуска пътното платно?
Задача № 2.4.30 от „Колекция от задачи за подготовка за приемни изпити по физика в USPTU“
Решението на проблема:
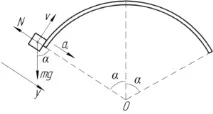
\[mg \cdot \cos \alpha - N = m\]
Ако в разглежданата точка автомобилът има скорост \(\upsilon\), тогава центростремителното ускорение \(a_ц\), действащо върху автомобила, може да се намери по формулата:
Ако в този момент автомобилът се откъсне от платното, тогава силата на реакция \(N\) ще бъде равна на нула. Предвид горното имаме:
В този случай скоростта на автомобила \(\upsilon\) може да се определи по формулата:
Всъщност открихме формула, която показва максималната скорост на автомобила, без да излиза от платното в произволна точка. Тази точка от обиколката на моста се определя от ъгъла \(\alpha\). Оказва се, че колкото по-голям е ъгълът \(\alpha\), толкова по-ниска е допустимата скорост. Това означава, че е по-вероятно колата да слезе от платното на входа на моста, отколкото в средата му (виж диаграмата).
От равенство (1) изразяваме ъгъла \(\alpha\):
Познавайки ъгъла \(\alpha\), е лесно да се намери дължината на моста, като се използва следната формула (имайте предвид, че ъгълът в тази формула е заменен в радиани, така че калкулаторът трябва да бъде настроен на RAD):
Нека преобразуваме скоростта в системата SI, след което изчислим отговора:
\[L = 2 \cdot 100 \cdot \arccos \left( ^2>>>>> \right) = 179\; м\]
Отговор:179 м
Ако сте харесали задачата и нейното решение, можете да я споделите с приятелите си чрез тези бутони.
2 мисли относно „Каква трябва да бъде максималната дължина на изпъкнал симетрик спрямо“
Не разбирам защо има arccos, а не 1/arccos? не трябва ли да е до c g
Специално за вас допълних решението, като описах по-подробно как намерих ъгъла α