Шпори от SR
Основи на теорията на еластичността и видове модели на реални среди.
Основи на теорията на еластичността - геоложки основи на сеизмичните проучвания - динамични особености и кинематични особености на разпространението на вълните - форма и уравнения на ходографите.
Под кинематични характеристики обикновено се разбира естеството на разпределението на вълновите или лъчевите фронтове и формата на ходографите, т.е. функции t(x) на времето на регистриране на трептенията от разстоянието между SP (точка на възбуждане) и RP (точка на приемане). Динамичните характеристики обикновено се разбират като естеството на промяната в амплитудите, честотите и, съответно, формата на записаните трептения.
Идеята на сеизмичното изследване: ние възбуждаме еластични вибрации в повърхностните води, те се разминават във всички посоки. Ако има твърди среди, върху които се променят физическите свойства на вълните, тогава вълните се отразяват и пречупват. Главните вълни и пречупените отново излизат на повърхността на Земята. Следователно теоретичната основа на SR е познаването на естеството на разпространението на еластичните вибрации. Източникът на трептения са или експлозии, или специални барабани, с други думи, някакви външни сили (фиг. 1.1.). Тези външни сили действат съответно върху скалите и се стремят да променят размера и формата на елементарните обеми на средата. С други думи, външните сили водят до създаване на деформации в средата, но всяка среда се противопоставя на външните влияния с вътрешни кохезионни сили между частиците и съответно се стреми да се върне в първоначалното си положение. Мярката за промяна на формата и размера на телата е концепцията за относителни деформации, свойството на скалите да се съпротивляват на деформации се нарича еластичност. Мярката за въздействието на външните сили върху скалите се нарича напрежение, т.е. количеството сила, действаща на единица площ. Освен това напреженията са нормални итангенциални (напрежения на срязване) (Фигура 1.2.). Когато дадена сила действа под някакъв ъгъл спрямо мястото, тя обикновено се разлага на няколко компонента или компоненти на тази сила. В този случай можем да изследваме проекциите или силовите компоненти върху съответните координатни оси.
Напреженията, възникващи в точка O (PV) и съответните им деформации се разпространяват в средата и създават процеса на разпространение на вибрациите. За описание на процеса на разпространение на вълната широко се използва законът на Хук, който установява връзката между напреженията и деформациите на средата. Формата на този закон зависи от сложността на структурата на средата. Ако тази връзка е линейна, което обикновено се наблюдава на практика, когато напреженията и деформациите са малки, тогава такива тела обикновено се наричат идеално еластични или абсолютно еластични. В този случай, след като премине през трептенията, средата се връща в първоначалното си състояние. Тези. няма остатъчни деформации. Ако напреженията се увеличат над границата на еластичност, тогава законът на Хук не е изпълнен и връзката между напреженията и деформациите ще бъде много по-сложна и такива тела се наричат пластични или неабсолютно еластични. Това се случва, когато експлозивите са източник на вибрации. При работа с експлозиви те се заравят в кладенеца, за да не се създават повърхностни вълни (Фигура 1.3.). В общото приближение геоложките среди се считат за абсолютно еластични. От тази гледна точка абсолютно еластичните среди често се подразделят на изотропни и анизотропни. Скалите се различават по скорост на разпространение на вълните и плътност: където V е скоростта, ρ е плътността, g е акустичната коравина. Изотропна среда е, когато свойствата на скалите не зависят от посоката. Анизотропните среди са среди, в които скоростите на еластичните трептения зависят от азимута (посоката) на технитеразпределение (Фигура 1.4). Освен това реалните среди могат да бъдат хомогенни и нехомогенни. При хомогенни. В хомогенните среди еластичните свойства са еднакви във всички точки на средата. В нехомогенни среди свойствата се променят.
През последните години беше въведена концепцията за дискретни медии (прекъснати или прекъснати). За разлика от непрекъснатите медии, свойствата на дискретните медии могат да се променят драстично от точка до точка. Най-често дискретните среди включват гранулирани, напукани или порести скали. По този начин в SR се използват широко различни модели медии (фиг. 1.5). Колкото по-сложен е моделът, толкова по-точно можем да опишем реалната среда, но колкото по-опростен е моделът, толкова по-удобен е за работа. Следователно изборът на модел винаги е някакъв компромис между способността за точно решаване на проблема и желанието той да бъде решен бързо и лесно. Ясно е, че най-простият модел е хомогенен, изотропен, еластичен, непрекъснат и е най-широко използван в СР. Горните модели на таблицата описват макроструктурата на скалите и съответно долните модели описват основно микроструктурата.
Концепцията за стрес и напрежение.
За да се изчислят стойностите на деформациите, обикновено се установява естеството на връзката между напреженията σ и деформациите ε. Теорията на SR се основава на закона на Хук, който определя връзката между напреженията и деформациите. Има нормални и срязващи напрежения. За напрежения на натиск или опън и едномерен модел на среда законът на Хук обикновено изглежда така:
Където C е определен коефициент на пропорционалност, който е някои физически и механични коефициенти, например модул на Йънг или коефициенти на Ламе. Ако имаме напрежения на срязване τ, тогава в този случай законът на Хук изглежда по същия начин, но само като коефициентпропорционалността обикновено е модулът на срязване. За математическото описание на напреженията, възникващи в твърдо тяло, широко се използва така нареченият тензор на напрежението, т.е. изображения на вектора на напрежението в някаква координатна система. За да направите това, във всяка точка на тялото обикновено се разглеждат три вектора σx, σy, σz, всеки от които се разлага на три компонента в зависимост от естеството на осите. Ако обозначим компонентите Ux, Uy, Uz на вектора на изместване U, тогава можем да напишем за тези компоненти:
Сумата от тези компоненти ще ни даде обемна деформация, която се нарича дилотация θ.
Съответно деформациите на срязване ще бъдат изразени със следните изрази:
Ако в тези формули вместо + има -, тогава те ще опишат въртене около една или друга ос, например:
В същото време трябва да се отбележи, че изрази 1.1 и 1.3 се използват, когато деформациите са малки, така че техните квадрати и произведения също са много малки и могат да бъдат пренебрегнати при изчисленията, т.е. смятат за равно на нула. Ето защо обикновено се счита, че преместването на частиците на средата е линейно, което е напълно приложимо за СР.
Уравнение на състоянието на средата.
В случай на произволни анизотропни еластични среди, всеки компонент на напрежението σij е свързан с компонента на деформация чрез съответните модули: . За триизмерно пространство тази връзка в математическа форма обикновено се записва в матрична (таблична) форма като тензор:
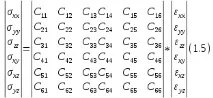
Ако вземем изотропна среда, тогава 24 коефициента на матрицата от 36 изчезват:

Ако тези коефициенти C се заменят със съответните константи на Ламе λ (характеризира устойчивостта на средата на натиск-опън) и μ (характеризира устойчивостта на средата на срязване). Ако тензорът се замени с прости уравнения, тези уравненияще изглежда така:
Където съответните напрежения са свързани с деформациите, като се използват константите на Lame. В едномерния вариант, т.е. за една пространствена координата, за изотропна среда, за нормални и тангенциални напрежения, човек може да напише формулите: или, които могат да се разглеждат, точно като уравнения 1.7 и 1.6, уравненията на състоянието на средата и те просто ни дават връзка между напреженията и съответните им деформации.
Еластични модули, използвани в теорията на сеизмичните проучвания.
За характеризиране на средата се използват различни еластични константи или модули. По-специално, модулите на Lamé μ и λ се използват широко за описание на обемни деформации в теоретичните изследвания. Модулът μ изразява съпротивлението на средата на срязване (коравина на срязване), а λ характеризира съпротивлението на средата при чист опън или натиск. В сеизмичните проучвания широко се използват и така наречените физико-механични или инженерни модули, които включват модула на Юнг Е и коефициента на Поасон ν. Модулът на Юнг характеризира съпротивлението при едноосно натиск или опън. Коефициентът на Поасон ν характеризира съотношението на деформацията към нейното удължение под действието на силите на опън. Понякога се казва, че коефициентът на Поасон установява връзката между твърдостта на срязване и съпротивлението на средата към деформации без срязване. Обикновено 0