Sopromat - решаване на проблеми
меню на сайта
Он-лайн изчисляване на геометричните характеристики на сечениятаНОВО- изчислява всякакви сечения (комплексно). Определя: площ на напречното сечение, инерционни моменти, моменти на съпротивление.
Онлайн изчисление на якост на греди- начертаване на Mx, Qy диаграми, намиране на максимален огъващ момент Mx, максимална сила на срязване Qy, изчисляване на деформации, избор на профил и др. Всичко е просто, всичко е онлайн. + Пълнобоядисано решение! Сега и застатически неопределенигреди!
Онлайн изчисление на рамки, греди фермиНОВО- Q, M, N диаграми, премествания на възли. Удобен графичен интерфейс. Разглежда всякакви схеми.
Лекции - теория, практика, задачи.
Справочна информация - GOSTs, гама от валцувани продукти, свойства на материалите и др.
Програми за якост на материалите (диаграми, различни калкулатори, шпори и др.).
Книги - различна литература по темата.
Основен курс от лекции по съпротивление на материалите, теория, практика, задачи.
2.5. Усукване на тънкостенни пръти със затворен профил.
Значително по-твърди и следователно по-подходящи при усукване са тънкостенните пръти със затворен профил.
Помислете за цилиндричен прът, чието напречно сечение е показано на фиг. 2.14. Дебелината на стената ще се счита за плавно променяща се по линията на контура, така че концентрацията на напрежението може да се пренебрегне.
Геометричното място на точките, еднакво отдалечени от външния и вътрешния контур на напречното сечение, се нарича средна линия на сечението.
Поради незначителната дебелина на стената може да се предположи, че тангенциалните напрежения, възникващи при усукване, ще бъдат равномерно разпределени по дебелината на стената и насочени тангенциално към централната линия на сечението.
Могапоказват също, че произведението на напрежението на срязване във всяка точка на стената и нейната дебелина е стойност, която е постоянна за всички точки от аксиалната линия на контура на сечението, т.е.
За да направите това, достатъчно е да разгледате състоянието на равновесие на всеки елемент от пръта, например елемент 1234 (фиг. 2.14).
В надлъжното сечение 1-4 има двойно напрежение на срязване, в сечение 2-3 - двойно напрежение на срязване
Проектирайки силите, действащи върху елемента върху посоката на оста на пръта, получаваме .
Тъй като точки 3 и 4 са взети произволно, тогава
Сега е възможно да се свърже големината на напрежението на срязване с въртящия момент, който възниква в сечението.
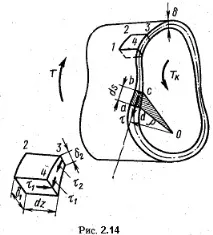
Силата, действаща върху елементарна площ (фиг. 2.14), очевидно е равна на, а въртящият момент на тази елементарна сила спрямо произволна точка O, лежаща в равнината на сечението, е равен на спрямо точка O.
Сумата от моментите около оста, успоредна на образуващата на пръта и минаваща през точка O, е равна на въртящия момент
където интегрирането се простира по цялата дължина на контура s; но продуктът pds е равен на удвоената площ на триъгълника O ab; pds = 2dA. следователно
Продуктът, като константа, може да бъде изваден от интегралния знак. Под интеграла остава изразът, който е площта на непрекъснат участък, ограничен от средната линия на участъка. Тогава
(2,36)
(2,37)
Най-голямото напрежение ще бъде на мястото, където дебелината на стената е минимална.
(2,38)
Ъгълът на усукване за прът с дължина l се определя от условието, че работата на външния усукващ момент е равна на работата на вътрешните сили. Работата на външен статично приложен момент върху ъгловото преместване е равна на
Нека сега изчислим потенциалната енергия на деформация,числено равно на работата на вътрешните сили.
Потенциалната енергия за елемент с обем ще бъде
където l е дължината на пръта.
Общата енергия на потенциалната енергия за целия прът е равна на
Интегрирането се извършва по дължината s на контура на сечението.
Заменяйки го със стойността от формула (2.37), намираме
Изваждаме константите извън знака за интеграл
Като вземем предвид, че потенциалната енергия U е числено равна на работата W на външния момент, получаваме T c = T
(2,39)
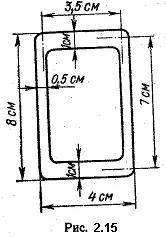
Пример 2.3.Определете максималното напрежение и ъгъла на усукване на тръбния прът (фиг. 2.15), ако T c = T = 1500 N * m, G = 80000 MPa.
Решение. По формула (2.38) намираме
Използвайки формула (2.39), определяме ъгъла на усукване на дължина от 1 m
Пример 2.4.Определете максималното напрежение и ъгъла на усукване на същия прът, ако профилът е отворен (т.е. ако контурът е изрязан на едно място).
Решение. Напрежението се определя по формулата (2.34):
Обърнете внимание, че този резултат има смисъл само за прът, изработен от легирана стомана, който има граница на пропорционалност при чисто срязване не по-ниска от намерената стойност, тъй като всички формули от тази глава са валидни само в обхвата на закона на Хук.
Ъгълът на усукване се определя по формулата (2.35)
Сравнението на резултатите от двата разгледани примера потвърждава предимствата на прътите със затворен профил в сравнение с прътите с отворен профил при работа на усукване.