Степенна функция, нейните свойства и графика - Studiopedia

Преобразуване на функционални графики

Съдържание:

1. Степенна функция, нейните свойства и графика;

- Симетрия спрямо координатните оси;

- Симетрия относно произхода;

- Симетрия спрямо правата y = x;

- Разтягане и свиване по координатните оси.

3. Показателна функция, нейните свойства и графика, подобни трансформации;

5. Тригонометрична функция, нейните свойства и графика, подобни трансформации (y = sin x; y = cos x; y = tg x);

Функция: y = x\n - нейните свойства и графика.

Степенна функция, нейните свойства и графика

y = x, y = x 2, y = x 3, y = 1 / x и т.н. Всички тези функции са специални случаи на степенна функция, т.е. функцията y = x p, където p е дадено реално число. Свойствата и графиката на степенна функция по същество зависят от свойствата на степен с реален показател и по-специално от стойностите на x и p, за които степента x p има смисъл. Нека пристъпим към подобно разглеждане на различни случаи в зависимост от показателя p.

1. Показателят p = 2n е четно естествено число.

В този случай степенната функция y = x 2n, където n е естествено число, има следните свойства:

• домейнът на дефиницията е всички реални числа, т.е. множеството R;
• набор от стойности - неотрицателни числа, т.е. y е по-голямо или равно на 0;
• функцията y = x 2n е четна, тъй като x 2n = (-x) 2n
• функцията е намаляваща на интервала x 0.

Графиката на функцията y = x 2n има същата форма като например графиката на функцията y = x 4 .

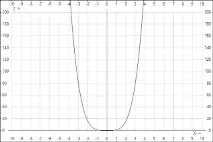
2. Показателят p = 2n - 1 е нечетно естествено число

В този случайстепенна функция y = x 2n-1, където е естествено число, има следните свойства:

• област на дефиниране - набор R;
• набор от стойности - набор R;
• функцията y = x 2n-1 е нечетна, защото (-x) 2n-1 = x 2n-1 ;
• функцията нараства по цялата реална ос.

Графиката на функцията y = x 2n-1 има същата форма като например графиката на функцията y = x 3 .

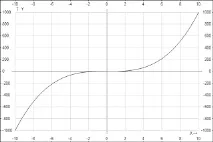
3. Показателят p = -2n, където n е естествено число.

В този случай степенната функция y = x -2n = 1/x 2n има следните свойства:

• областта на дефиниция е множеството R, с изключение на x = 0;
• набор от стойности - положителни числа y>0;
• функцията y = 1/x 2n е четна, тъй като 1/(-x) 2n = 1/x 2n ;
• функцията нараства на интервала x0.

Графиката на функцията y = 1/x 2n има същата форма като например графиката на функцията y = 1/x 2 .

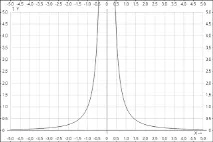
4. Показателят p = -(2n-1), където n е естествено число. В този случай степенната функция y = x -(2n-1) има следните свойства:

• областта на дефиниция е множеството R, с изключение на x = 0;
• набор от стойности - набор R, с изключение на y = 0;
• функцията y = x -(2n-1) е нечетна, тъй като (-x) -(2n-1) = -x -(2n-1) ;
• функцията намалява на интервали x 0.

Графиката на функцията y = x -(2n-1) има същата форма като например графиката на функцията y = 1/x 3 .

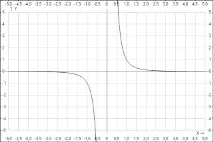
Не намерихте това, което търсихте? Използвайте търсачката:

Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо

---