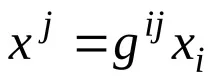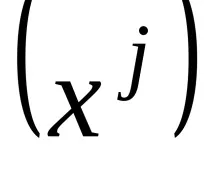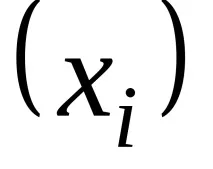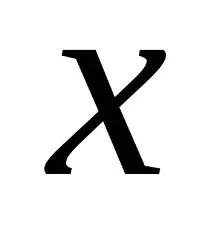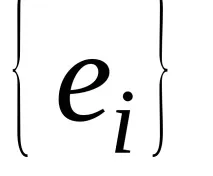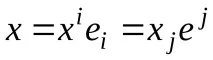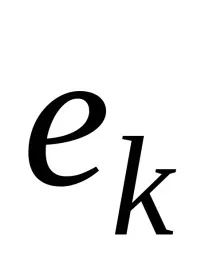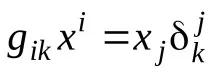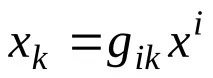tensors_eucl_space.doc
§18. Тензори в евклидовото пространство.
1º. Фундаментален метричен тензор.
Дефиниция 1. Свържете всеки базис
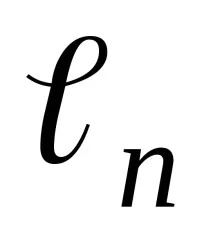
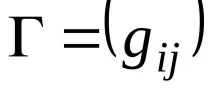
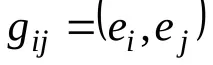

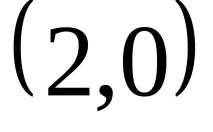
Д.З. Докажете, че

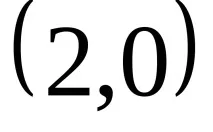
В примера, обсъден в 1º, беше показан параграф 16. Че компонентите на матрицата
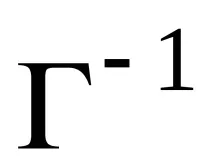
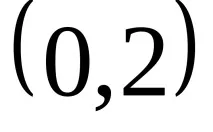
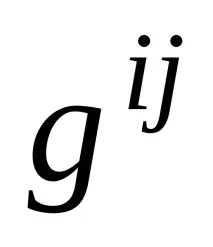
Д.З. Докажи отново.
Дефиниция 2. Тензор с
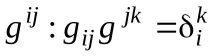

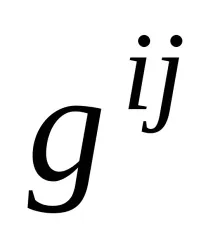
2º. Повишаване и понижаване на индекси.
Когато индексът е пропуснат, тензор от тип
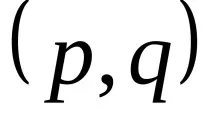
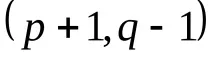
Например
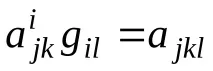
Когато индексът се повиши, даденият тензор се свива с контравариантния метричен тензор при индекса, който трябва да се повиши. Резултатът ще бъде тензор от тип
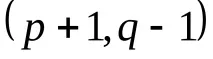
Например
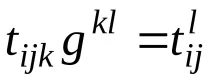
3º. Евклидови тензори.
Когато изучавате евклидовото пространство, можете да се ограничите до разглеждането на ортонормалните бази. Тогава матриците на прехода в този случай са ортогонални, т.е. отговарят на отношението
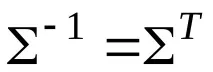
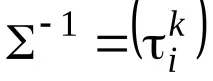
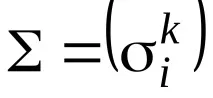
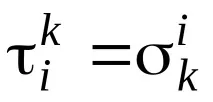
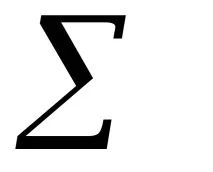
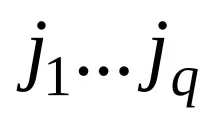
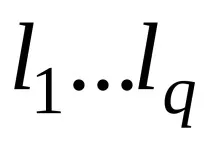
Тъй като в ортонормална основа
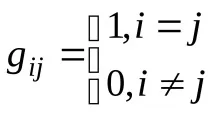
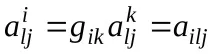
От казаното следва, че ограничавайки се до ортонормална основа, можем да идентифицираме всички тензори, получени един от друг чрез повишаване или понижаване на индекса. Наборът от такива еквивалентни тензори се нарича Евклидов тензор.
Евклидовият тензор се определя от валентност

Стойностите, които се запазват при преминаване от една ортонормална основа към друга, по-рано наричахме ортогонални инварианти. По този начин ортогоналните инварианти са евклидовите валентни тензори
Евклидовите тензори могат да бъдат сгънати, редуващи се и симетрични върху всяка двойка индекси.
Важен пример за евклидовия тензор е дискриминантният тензор, дефиниран за някакъв ортонормален базис чрез равенството:

При преминаване към друга основа имаме:
, т.е. показа, че компонентите на дискриминантния тензор са еднакви във всички ортонормални бази със същата ориентация с оригиналните и се различават по знак в бази с противоположна ориентация.
За неортонормални бази евклидовите тензори се разширяват.
4. Контравариантни и ковариантни векторни компоненти.
Да разгледаме контавариантен вектор от тип
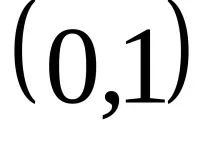
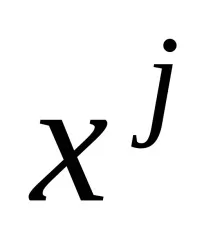
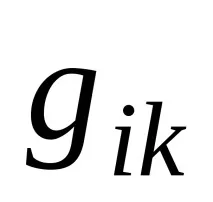
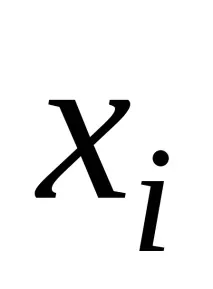

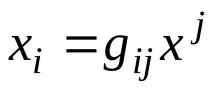
В същото време