Тервер отговаря 37 - 1
1. Класификация на случайни събития: възможни и невъзможни събития, съвместни и несъвместими, противоположни и определени събития. Примери.
Пространство от елементарни събития Всеки от еднакво вероятните резултати от теста се наричаелементарен резултатили (елементарно събитие). Всеки възможен резултат от експеримент се нарича елементарно събитие и обикновено се обозначава с буквитеПространството от елементарни събитияе съвкупността от всички взаимно изключващи се резултати от експеримента, така че резултатът от експеримента винаги е един и само един резултат. Пространството от елементарни събития обикновено се обозначава и се счита за дадено, ако всички негови елементи са посочени. От елементарни резултати може да се състави по-сложно събитие. Резултатът от теста се наричасъбитие, независимо от неговата значимост. Резултатът от теста, който не може да бъде предвиден предварително, се наричаслучайно събитие. Всяко подмножество от този набор се интерпретира като събитие (вероятно ненаблюдаемо). Съвкупността от всички наблюдавани събития съставлява набора от събитияза този експеримент. Наборът за този тест може да бъде отделен или да има по-сложна структура. Дискретни са крайни или преброими набори от елементарни резултати. Изграждането на набора (ако не е посочено в описанието на експеримента) се извършва на практика, въз основа на изискването всички резултати от този интересен за нас експеримент да могат да бъдат еднозначно описани на базата на конструирания набор. С други думи, ако се интересуваме от събитияи т.н.,които са наблюдавани събития в този експеримент, тогава наборът трябва да се състои от такива резултати, че има подмножества от този набор, които са еквивалентни на събития и т.н.
Настъпване на събитие, благоприятни резултатиВсяко случайно събитие се определя като подмножество в набора от елементарни събития. Освен това тези елементарни събития от , при които събитието се случва (т.е. принадлежи към подмножеството ), се наричат благоприятниза събитието . Казват, че дадено събитие се е случило (дошло, станало, било реализирано), ако резултатът от експеримента е елементарен резултат, принадлежащ на ().Съвместими (съвместими), несъвместими (несъвместими) събитияДве събития се наричат съвместими(съвместими) в този експеримент, ако появата на едно от тях не изключва появата на другото. Две събития се наричат в съвместими(несъвместими) в този експеримент, ако не могат да се появят заедно в едно и също изпитване. Няколко събития се наричат несъвместими, ако са несъвместими по двойки. С други думи, събитията са едновременно съвместими, ако съответните множества и имат общи елементи, и иначе несъвместими, ако появата на едно от тях изключва появата на другото, и съответните множества и нямат общи елементи, т.е. пресечната точка на тези множества е празното множество.
Надеждни и невъзможни събитияНадеждние събитие, което определено ще се случи, ако е изпълнен определен набор от условия.
Събитие, което съответства на празния набор, се наричаневъзможносъбитие, а събитие, което съответства на целия набор, се наричанадеждносъбитие. Събитията се наричат еднакво възможни, ако няма причина да се смята, че едно събитие е по-вероятно от други.
Теорията на вероятностите е наука, която изучава моделите на случайни събития. Един от основните проблеми в теорията на вероятностите е проблемът за определяне на количествена мярка за възможността за възникване на събитие.
2. Пълна група от събития. Пространство на елементарни резултати. Примери.
Пълна група от събития. Пълна група от събития е съвкупността от всички възможни резултати от експеримент.Теорема.Сумата от вероятностите за събитияА1 , А2 , . An ,образуващ пълна група, е равен на едно:
Пространство на елементарни резултати
Теорията на вероятностите изучава случайни явления не директно, а с помощта на идеализирани математически моделина случайни експерименти.
Всеки случаен опит (тест,експеримент) се състои в прилагането на определен набор от условия и наблюдението на резултата. Всеки наблюдаван резултат от експеримента се интерпретира катослучаен резултат(случайно събитие). Случайно събитие в резултат на опит може да се случи или да не се случи.
На всеки опит се присвоявапространство от елементарни резултати. Това е набор от най-простите (т.е. неразложими в рамките на даден експеримент на по-прости) взаимно изключващи се резултати, така че резултатът от експеримента винаги е един и само един резултат.
Опитътсе състои от хвърляне на един обикновен шестстранен зар и наблюдение на броя на хвърлените точки.
Неелементарни резултати(събития): =, = и т.н. Резултатът не е елементарен, т.к той се разлага на по-прости резултати.
Пространство на елементарни резултатиТова произволно преживяване се състои от шест елемента.
3. Класическата дефиниция на вероятността от събитие. Вероятностни свойства на събитие. Примери.
Вероятността за събитие е съотношението на броя на елементарните резултати, които благоприятстват дадено събитие, към броя на всички еднакво възможни резултати от опит, в които това събитие може да се появи. Вероятността за събитие A се означава с P(A). В съответствие с определението P(A)=m/n, където m е броят на елементарните резултати, които благоприятстват събитие A; n е броят на всички еднакво възможни елементарни резултати от опит, които образуват пълна група от събития. Това определение на вероятността се нарича класическо.
Основни свойства на вероятността.Нека е дадено пространството от елементарни събитияEи вероятноститеPда бъдат дефинирани върху събития отE. Тогава:
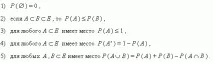
Една урна съдържа 10 топки с еднакъв размер и тегло, от които 4 са червени и 6 са сини. От урната се изтегля една топка. Каква е вероятността изтеглената топка да е синя?
Решение. Събитието „извадената топка се оказа синя“ ще бъде отбелязано с буквата A. Този опит има 10 еднакво възможни елементарни изхода, от които 6 са в полза на събитието A. В съответствие с формулата P(A)=m/n получаваме P(A)=6/10=0.6
4. Статистическо определяне на вероятността от събитие. Примери. Теорема на Бернули (с доказателство).
Статистическата вероятностна събитие А е относителната честота (честота) на възникване на това събитие в n теста, т.е.
w(A) е относителната честота (честота) на събитие A;
m е броят опити, в които се появи събитие А;
n е общият брой опити.
Статистическата дефиниция на вероятността, както и концепциите и методите на теорията на вероятностите са приложими само за тезисъбития, които имат свойства:
- Разглежданите събития трябвада бъдат резултатите само от тези опити, които могат да бъдат възпроизведени неограничен брой пъти при един и същи набор от условия.
- Събитията трябва да иматстатистическа стабилностилиотносителна стабилност на честотата. Това означава, че в серия от тестове относителната честота на дадено събитие не се променя значително.
- Броят на опитите, в резултат на които възниква събитието А,трябва да бъде достатъчно голям, тъй като само в този случай вероятността на събитието P(A) може да се счита за приблизително равна на неговата относителна честота.
W(A) = = 0,5005
Честотата на събитие вnповтарящи се независими опити, във всяко от които то може да се случи с една и съща вероятностp, с неограничено увеличение на брояnсе сближава по вероятност с вероятносттарна това събитие в отделен опит:
Смисълът на теоремата е, че при голям бройnповторени независими опити е практически сигурно, че честотата на събитиетоm/nе случайна стойност, произволно малко се различава от неслучайната стойностp- вероятността на събитието, т.е. на практика престава да бъде случаен.