Точка в 3d пространство»
по дисциплина "Компютърна графика"
Студентска група МО-305
Професор в катедрата на ВМИК
Съдържание
1. Смислено и формално изложение на проблема 3
1.1 Смислено изложение на проблема. 3
1.2.Формално изложение на проблема. 3
2. Кратка теоретична информация 4
4.3 Рендиране (чертане на чертежи на екрана). 12
5.1 Разширен алгоритъм 15
5.1.1 Въвеждане на данни. 15
а) Координатни изчисления за пространствен чертеж. 15
б) Изчисляване на координати за сложен чертеж. 16
5.1.3 Рендиране (чертане на чертежи на екрана). 16
а) Начертаване на пространствена рисунка. 16
б) Рисуване на сложен чертеж. 16
5.2 Подробен алгоритъм 17
5.2.1 Въвеждане на данни. 17
а) Координатни изчисления за пространствен чертеж. 17
б) Изчисляване на координати за сложен чертеж. 18
5.2.3 Рендиране (чертане на чертежи на екрана). 18
а) Начертаване на пространствена рисунка. 18
б) Рисуване на сложен чертеж. 19
6.Ръководство на програмиста 21
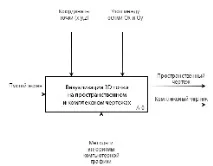
Когато програмата стартира, в конструктора Form1 се създават екземпляри на Point3D, клас Point, масиви от точки points3D, points3D_disp, pointsComplex_disp. Масивът points3D се попълва в метода input(). След инициализацията се извикват методи за преизчисляване на координатите на чертежа. За пространствен чертеж преобразуването в екранната система се извършва в метода Area(): стойностите се записват в масива points3D_disp, който използва функцията за преизчисляване Projection3D(points3D[i]), където елементите на масива points3D се предават на функцията като параметри. За сложен чертеж преобразуването в екранната система се извършва в метода Complex(): стойностите се записват в масива pointsComplex_disp,който използва функцията за преизчисляване ProjectionComplex(x,y), където елементи от масива points3D се предават като параметри на функцията. След това се извършва рисуване, за да се покаже оригиналният чертеж в pb3D и pbComplex, като се използват съответно функциите Draw3D(), DrawComplex(). 24
7. Ръководство за потребителя 25
Смислено и формално изложение на проблема
Съдържание на проблема.
пространствен чертеж, изобразяващ точка T, нейните проекции върху координатните равнини T1, T2, T3 и проекциите й върху координатните оси TX, TY, TZ, както и комуникационни линии;
комплексен чертеж, показващ проекциите на точка Т - Т1, Т2, Т3, както и комуникационни линии;
плъзгащи се превключватели за интерактивна промяна на координатите на точката Т и ъгъла между осите Ox и Oy в пространствен чертеж.
когато се променят координатите на точката Т, нейното изображение, изображенията на нейните проекции и комуникационни линии трябва да се променят както на пространствените, така и на комплексните чертежи;
при промяна на ъгъла между осите Ox и Oy пространственият чертеж трябва да се преначертае.
Официално изложение на проблема.
Кратка теоретична информация
Проекционната операция е в основата на конструирането на всяко изображение.
Същността на метода на ортогоналната проекция се състои в това, че обектът се проектира върху две взаимно перпендикулярни равнини чрез лъчи, ортогонални (перпендикулярни) на тези оси.
Една от проекционните равнини P1 е разположена хоризонтално, а втората P2 - вертикално. Равнината P1 се нарича хоризонтална равнина на проекциите, P2 - фронтална. Равнините P1 и P2 са безкрайни и непрозрачни.
Когато конструирате проекции, трябва да се помни, че проекцията на точка върху равнина е основата на перпендикуляра, пуснат от даденаточки на тази равнина. Проекцията на точка Т върху хоризонталната равнина се нарича хоризонтална проекция и се означава като Т1, проекцията на точка Т върху фронталната равнина се нарича фронтална проекция и се означава като Т2. Всяка от тях е основата на перпендикуляра, пуснат от дадената точка T съответно върху равнините P1 и P2. Две проекции на една точка определят нейното положение в пространството. Тъй като всяка фигура или тяло е набор от точки, може да се твърди, че две ортогонални проекции напълно определят неговата форма.
Въпреки това, в практиката на изобразяване на строителни конструкции, машини и различни инженерни конструкции, става необходимо да се създават допълнителни проекции. За да направи чертежа на проекцията по-ясен и по-четим, се използва трета равнина, перпендикулярна на P1 и P2. Тази равнина се обозначава с буквата P3 и се нарича профилна равнина. Проекцията на точката T върху равнината P3 се нарича профилна проекция и се означава с T3.
Проекционните равнини, пресичащи се по двойки, определят три оси: Ox, Oy и Oz, които могат да се разглеждат като система от правоъгълни декартови координати в пространството с начало в точка O. Три проекционни равнини разделят пространството на осем тристенни ъгъла - това са така наречените октанти. Номерацията на октантите е дадена на фиг. 1.
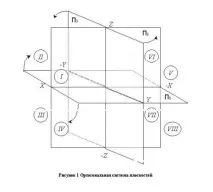
Като се имат предвид ортогоналните проекции, се приема, че наблюдателят е в първия октант. Проекционен чертеж, в който проекционните равнини с всичко, което е изобразено върху тях, се комбинират по определен начин една с друга, се нарича диаграма на Монж (просто диаграма или сложен чертеж). За да се получи диаграма, равнините P1 и P3 се завъртат, както е показано на фиг. 1 до подравняване с равнината P2. В резултат на въртене предната полуравнина P1 е подравнена сдолната полуравнина P2, а задната полуравнина P1 - с горната полуравнина P2. Крайният изглед на всички комбинирани проекционни равнини е даден на фиг. 2.
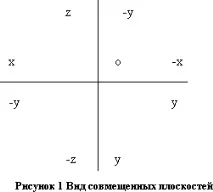
Координатите са числа, които съответстват на точка, за да се определи нейната позиция в пространството или върху повърхност.
В триизмерното пространство позицията на точка се задава с помощта на правоъгълни декартови координати x, y, z. Абсцисата x определя разстоянието от дадената точка до равнината P3, ординатата y до равнината P2, а апликацията z до равнината P1.
Препоръчително е да се изгради изображение на самата точка и нейните проекции върху пространствен модел с помощта на координатен правоъгълен паралелепипед. Първо, сегментите се нанасят върху координатните оси от точка O, съответно равни на единици дължина. На тези сегменти (OTX, OTY, OTZ), както на ръбове, е изграден правоъгълен паралелепипед. Неговият връх, срещу началото, ще определи дадената точка T.
Конструкцията на паралелепипед ни позволява да определим не само точката Т, но и трите й ортогонални проекции.
Лъчите, проектиращи точка върху равнините P1, P2 и P3, са онези три ръба на паралелепипеда, които се пресичат в точката T.
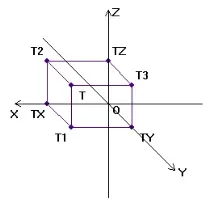
На диаграмата, където всички проекционни равнини са подравнени, проекциите T1 и T2 ще бъдат на същия перпендикуляр на оста OX, а проекциите T2 и T3 ще бъдат на същия перпендикуляр на оста OZ. Що се отнася до проекциите T1 и T3, те също са свързани с прави линии T1TY и T3TX, перпендикулярни на оста OY. Но тъй като тази ос заема две позиции на диаграмата, сегментът T1TY не може да бъде продължение на сегмента T3TY.
Построяването на проекциите на точка Т върху диаграмата по зададените координати се извършва в такъвпоследователности: първо на абсцисната ос от началото се начертава сегментът OTX = x и след това се изчертава перпендикуляр на оста Ox през точката TX, върху която, като се вземат предвид знаците, се нанасят сегментите TXT1 = y (получаваме T1) и TXT2 = z (получаваме T2). Остава да се построи профилната проекция на точка Т3. Тъй като профилът и фронталните проекции на точката трябва да са разположени на един и същи перпендикуляр на оста Oz, през T2 се изчертава права линия T2TZ, перпендикулярна на Oz. И накрая, възниква последният въпрос: колко далеч от оста Oz трябва да бъде T3? Като се има предвид координатната кутия, чиито краища са TZT3 = OTY = TXT1 = y, заключаваме, че желаното разстояние TZT3 е равно на y. Сегментът TZT3 се поставя отдясно на оста Oz, ако y>gt; 0 и наляво, ако y
За да се изобрази пространствен чертеж, е необходимо триизмерните координати да се трансформират в двумерна екранна координатна система. Изходната точка на екрана е горният ляв ъгъл. Ширината и височината на екрана се записват в константите w, h. (фиг. 5)
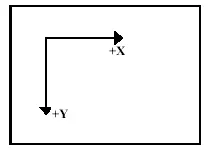
Координатите на началото на пространствения чертеж O в най-простия случай могат да бъдат намерени, както следва:
По този начин е необходимо да се изведат формули за преобразуване на зададените триизмерни координати на произволна точка T x, y, z в двумерни екранни координати xе, ye, като се вземат предвид дадения ъгъл ъгъл и координатите на началото - x0, y0.
Помислете за следната фигура.
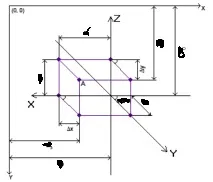
От тази фигура се вижда, че и, където ∆x и ∆y се намират от съответните правоъгълни триъгълници съгласно формулите:
И така, получихме формули за изчисляване на екранните координати на произволна точка според дадените триизмерни координати, ъгъл ъгъл и координати на началотосправка. Използвайки тези формули, можете да изчислите координатите на точките, необходими за изграждане на пространствен чертеж - T, T1, T2, T3, TX, TY, TZ.
Изчислете екранните координати на референтната точка на пространствения чертеж по формули (1);
Изчислете координатите на самата точка, нейните проекции върху координатните оси и равнините P1, P2, P3, като използвате формули (2).
Изчисляване на координати за множество чертежи.
координати на точка Т в 3D декартова координатна система – x, y, z
ширина и височина на чертежа - ш и в.
екранни координати на началото на сложния чертеж;
координати на точките на комплексния чертеж: T1, T2, T3 (проекции на точка T върху P1, P2, P3), Tx, Ty1, Ty2, Tz (проекции на точка T върху оста, за оста Y - две такива точки, тъй като тя е представена два пъти в комплексния чертеж).
Координатите на началото x0, y0 се намират по формула (1).
Разгледайте следната фигура, разстоянията x, y, z на която са посочени в съответствие с конструкцията на сложен чертеж.
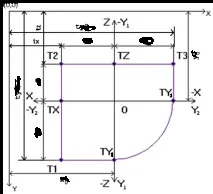
От снимката можете да видите, че:
Имайте предвид, че координатите на всички точки, които ни интересуват, могат да бъдат намерени от стойностите x0, y0, tx, tz, ty1, ty2:
изчислете координатите на началото по формулите (1).
изчисляване на временни променливи с помощта на формули (3).
изчислете координатите на точковите проекции, като използвате формули (4).