Траектории на изравняване, Авиация - търговска, гражданска, специална авиация
В процеса на изравняване самолетът се движи по извита траектория, свързваща глисадата и права линия, успоредна или с лек наклон към земната повърхност. Кривината на траекторията възниква поради действието на центростремителната сила, която възниква с увеличаване на ъгъла на атака на самолета (фиг. 3.7.) •
ориз. 3.77. Сили, действащи върху sa- самолета по време на центровка

При K=const и rty=const траекторията на подравняване се представя от дъга от окръжност с радиус r. На практика се избягва рязка промяна в претоварването. Обикновено в началото на изравняването g-натоварването се увеличава плавно до предварително определена стойност и към края ясно намалява до n = 1. В допълнение, по време на процеса на изравняване самолетът забавя.
Следователно действителните траектории на подравняване са малко по-различни от дъгата на кръг. Въпреки това, за приблизителни анализи е напълно приемливо те да се считат за кръгови дъги с определен z-радиус.
Ъглова скорост на самолета по време на нивелиране > такива траектории се определя от уравнението
Тъй като пътят на подравняване представлява дъга, обхващаща ъгъл от 0gl, времето за подравняване
начало на изравняване на пчелна пита
Ориз. 3.78. Към връзката между радиуса на кривината r, височината на началото на трасето R и дължината на трасето L
Минималният радиус на кривина /mm на траекторията на подравняване и максималната ъглова скорост на клетките при дадена скорост V са ограничени от максимално допустимата стойност на претоварването на поставянето или увеличението на претоварването L /%gaax по време на тази маневра:
Допустимите G-сили при изравняване за пътнически самолети са приблизително еднакви. Следователно разликата между стойностите на минималните радиуси на кривина на траекториите на подравняване и ъгловискоростта на движение за различните типове самолети се дължи главно на разликата в техните скорости. Увеличаването на радиуса на кривината на траекторията при постоянен ъгъл на наклона на плъзгача води до увеличаване на височината на началото на центровката (фиг. 3.78). Следователно, при различни други условия, самолетите с високи скорости трябва да започнат да се изравняват на по-голяма надморска височина.
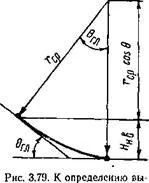
Да определим зависимостта на височината от началото на подравняването Jac. B от основните характеристики на движението, под които в този случай имаме предвид средните стойности на скоростта и претоварването или стъпките на претоварване в процеса на изравняване. От фиг. 3.79 показва това
^n, = ^(1-cos0Gl). (3,143)
Нека отбележим, че до същия резултат може да се стигне на базата на връзката £Ex
5= UsrNr- Стойността на ^0r се определя по формулата £(3.141).
Да предположим, че има два самолета със средни скорости на V7! и V2, и Vi
Ако приемем, че в края на подравняването R(/)=0, получаваме 1 = oo. ^ На практика разстоянието за подравняване е ограничено. Неговата w стойност обаче се оказва доста значителна. Тя може да бъде намалена, ако се приеме, че при контакт със земята самолетът има
някаква вертикална скорост Vyipii3(Hnris). В съответствие с - (3.146), самолетът има такава вертикална скорост на височина:
Следователно, за да може самолетът да има вертикална скорост Hpriz при кацане, е необходимо асимптотата на експонентата. беше под повърхността на пистата (виж Фигура 3.82) на разстояние; Rs се определя от зависимостта (3.153). При T = 2n-5 sec и Nprnsh = 0,3-y-0,6 m/sec, експоненциалната асимптота трябва да е под повърхността на пистата с #ac = 0,6-u3,0 m.
Дължината на разстоянието за центриране при кацане с вертикална скорост Yapriz
В този случай R0 е височината на началото на подравняването, броено от асимптотота на експонентата.Връзката му с височината на началото на трасето е ha. c, измерено от нивото на пистата, се вижда от фиг. 3.82 При нивелиране абсолютната стойност на вертикалната скорост a на функцията на височината H, измерена от нивото на асимптотота, се определя от уравнението
и абсолютната стойност на вертикалната скорост като функция на височината: h, измерена от нивото на пистата, се дава от уравнението
Графиката на изменението на вертикалната скорост е показана на фиг. 3,84.
Сега нека помислим каква ще бъде траекторията на изравняване на самолета, ако бъде засегнат от смущение. Нека се обърнем към фиг. 3,84. При липса на смущения изравнената траектория е експоненциална, минаваща през точка 1. Да приемем, че в резултат на действието на турбулентно смущение самолетът се премества от точка 1 до точка 2, след което действието се смущава;11: спира. По-нататъшното движение на самолета се извършва от експоненциална траектория, минаваща през точка 2, на равно разстояние от първоначалната траектория. Съответно ще се премести и точката на кацане на самолета. В тази връзка разгледаните по-горе траектории понякога се наричат "свободни и" траектории.
Досега говорихме за подравняването на самолета по различни видове траектории. Понастоящем е известен и методът за подравняване на софтуера. В този случай, като се започне от височината на началото на нивелацията, се задава промяна на програмата по време на един от параметрите на надлъжното движение на самолета. Като
Такъв параметър може да бъде избран, например ъгъл на тангаж или атака i, претоварване, ъгъл на отклонение на елеватора и т.н. Ако по време на настройката на програмата въздействат големи смущения върху самолета, може да се окаже, че в момента на кацане самолетът има неприемливо големи отклонения на параметрите на движение. За кацане на пътнически самолети този метод не е приложим -Гниещ