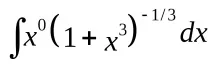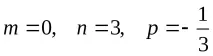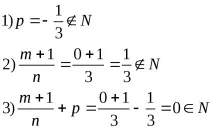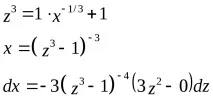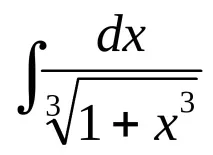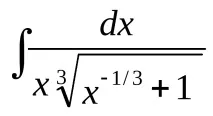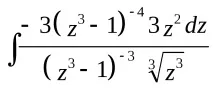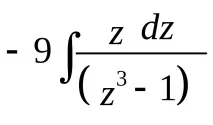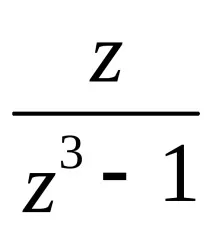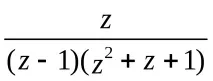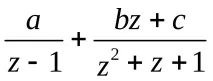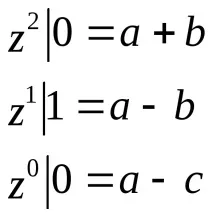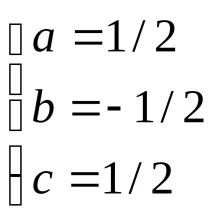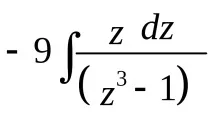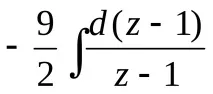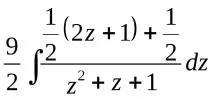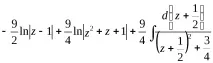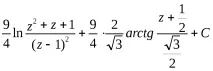Урок 10 Диференциално биномно интегриране
1.5.10. Интегриране на диференциален бином
Интеграл от диференциален бином
къдетоm,nиp-рационални числа, може да се сведе до интегриране на рационални функции само в следните три случая (теорема на Чебишев):
Случай 1. Некаpе цяло число. След това поставяме
, където
Nе общият знаменател на дроби
mи
n.
Случай 2. Нека
е цяло число. След това поставяме
, където
Nе знаменателят на
p.
Случай 3. Нека
е цяло число. След това прилагаме заместването, където
Nе знаменателят на дробта
p.
Ако
, тогава тези случаи са еквивалентни на следното:
№1985=нека пренапишем интегранта като диференциален бином=сега е ясно, че
. Нека се уверим, че този диференциален бином принадлежи към един от трите посочени случая.
Проверката показа, че заместването
ще доведе до рационална форма на интегранта. Наистина,
===,и проблемът се сведе до намирането на интеграла на правилна рационална дроб, която трябва да бъде представена като сбор от елементарни дроби.
=
=
=
Търсенето на интеграли на тези елементарни дроби е добре позната задача.
==+== ==
№ 1981, 1983, 1989 са решени по подобен начин.
Домашна№№ 1982, 1986, 1988.
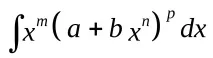
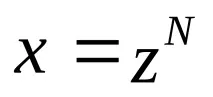
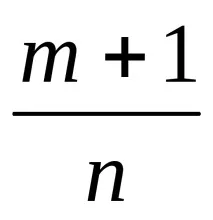
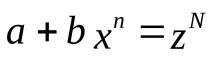
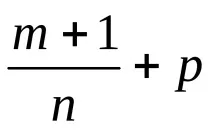
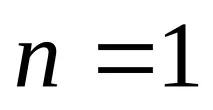
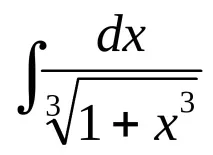 =сега е ясно, че
=сега е ясно, че