Векторно смятане
Значението на думата "Векторно смятане" в Голямата съветска енциклопедия
Векторно смятане, математическа дисциплина, която изучава свойствата на операциите върхувекториот евклидовото пространство. В същото време концепцията
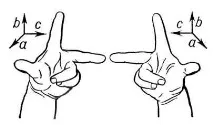 |
| Ориз. 6 към чл. Векторно смятане. |
Произход и развитиеВекторно смятане Появата наВекторно смятане е тясно свързано с нуждите на механиката и физиката. До 19 век само координатният метод беше използван за уточняване на вектори, а операциите върху вектори бяха сведени до операции върху техните координати. Едва в средата на 19в. с усилията на редица учени е създаденоВекторно смятане, в което операциите се извършват директно върху вектори, без да се прибягва до координатния метод на настройка. Основите наВекторното смятане са положени от изследванията на английския математик У. Хамилтън и немския математик Г. Грасман върху хиперкомплексните числа (1844-50). Техните идеи са използвани от английския физик Дж. К. Максуел в работата му върху електричеството и магнетизма. Модерният облик наВекторното смятане е даден от американския физик Дж. Гибс. Съществен принос за развитието наВекторното смятане имат български учени. На първо място трябва да се отбележат произведенията на М. В. Остроградски. Той доказа основната теорема на векторния анализ (вижформулата на Остроградски).Изследванията на казанския математик А. П. Котелников върху развитието навинтовото смятанебяха от голямо значение за механиката и геометрията. Тези изследвания бяха продължени от Съветския съюзматематиците Д. Н. Зейлигер и П. А. Широков. Голямо влияние върху развитието наВекторното смятане оказва книгата "Векторен анализ", написана през 1907 г. от българския математик П. О. Сомов.
Векторна алгебра. Векторът е насочен сегмент (фиг. 1 ), т.е. сегмент с определено начало (наричан още точка на приложение на вектора) и край. Дължината на насочен сегмент, представляващ вектор, се нарича дължина или модул на вектора. Дължината на вектораa се означава сa.Векторите се наричат колинеарни, ако лежат или на една права, или на успоредни прави. Два вектора се наричат равни, ако са колинеарни, имат еднаква дължина и еднаква посока. Всички нулеви вектори се считат за равни. Показано нафиг. 1 векторитеа иb са колинеарни и равни.Векторното смятане се занимава със свободни вектори.
Във векторната алгебра линейните операции върху вектори играят важна роля: операцията за добавяне на вектори и умножаване на вектор по реално число. Сумата отa +bна векторитеa иb е векторът, преминаващ от началото на вектораa до края на вектораb, при условие че началото на вектораb е прикрепено към края на вектораa (фиг. 2 ). Произходът на това правило е свързан с правилото на паралелограма за добавяне на вектори (Фиг. 3 ), чийто източник е експерименталният факт за добавяне на сили (векторни величини) съгласно това правило. Конструкцията на сумата от няколко вектора е ясна отфиг. 4. Произведениетоaана вектораа с числотоaе вектор, колинеарен на вектораа, с дължина равна на lal. la l и същата посока катоa, когатоa> 0 и срещуа сa