Всичко за Конус

Конусът е тяло, получено чрез въртене на правоъгълен триъгълник около права линия, съдържаща катет.

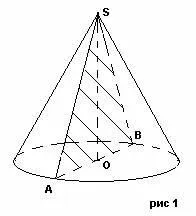
S - върха на конуса, кръг с център O - основата на конуса

Отсечка SA=L образуваща.

Отсечката OA=R е радиусът на основата.

Отсечка BC=2R – диаметър на основата.

Триъгълник SBC-осово сечение

Ъгъл BSC - ъгъл при върха на аксиалното сечение

Ъгъл SBO - ъгълът на наклона на генератора към равнината на основата

II Конусно сечение

1. Секущата равнина минава през оста на конуса (аксиално сечение - равнобедрен триъгълник фиг. 1)

2. Секущата равнина е перпендикулярна на оста на конуса

- кръг с център O1 (фиг. 2)

3. Сечението, минаващо през върха на конуса, е равнобедрен

триъгълник (фиг. 3)

4. Параболични и хиперболични сечения. (фиг. 4)

Сфера винаги може да бъде вписана в конус. Центърът му е върху оста на конуса

и съвпада с центъра на окръжността, вписана в триъгълник,

което е аксиалното сечение на конуса.

Rsh \u003d Rk * tg a / 2 \u003d H * Rk / Rk + L

Сфера винаги може да бъде описана близо до конус. Центърът му лежи върху

оста на конуса и съвпада с центъра на описаната окръжност

триъгълник, който е осово сечение на конус.

Rsh \u003d Rk / sinb; R²sh = (H-Rsh)² + Rk²

Rsh \u003d L / 2H; (2Rsh - Hk) Hk = Rk²

III Повърхностна площ на конуса

Площта на неговото развитие се приема като площ на страничната повърхност на конуса. Нека изразим страната на S по отношение на нейната рамка L и радиуса на основата r. Площта на кръговия сектор πL²/360*α . Изразяваме α чрез L и r. Дължината на дъгата ABA е 2πr (обиколката на основата на конуса) 2πr = πL/180* α, следователно α=360r/L, следователно Sside = πL²360r/360L=πrL

2. Пълна площповърхността на конуса е сумата от площите на страничната повърхност и основата

Обем на IV конус

Обемът на конус е равен на една трета от площта на основата, умножена по височината.

Да разгледаме конус с обем V, радиус R, височина h и връх O. Нека въведем оста Ox, така че да съвпадне с оста -OH на конуса. Произволно сечение на конуса с равнина, перпендикулярна на оста Ox, е окръжност с център в точката H1 от пресечната точка на тази равнина с оста Ox. Нека означим радиуса на тази окръжност с , φ площта на S(x) с , където x е абсцисата на точката H1. От подобието на триъгълници OH1A1 и IT следва, че OH1/OH=R1/R,

или x/h=R1/R=>R1=XR/h. Тъй като S(x)= πR², тогава S(x)= πR²/h²* ²

Прилагайки основната формула за изчисляване на обемите на телата при a=0 и b=h, получаваме

V пресечен конус.

Пресечен конус е част от конус, затворена между основата и част от конуса, успоредна на основата.

Кръгове с центрове O1 и O2 са горната и долната основа на пресечения конус, R r са радиусите на основите, AB \u003d L генератора, α е ъгълът на наклон на генератора и равнината на долната основа.

Сегмент O1O2-вис. Трапец ABCD - аксиално сечение.

H=L*sin α

Сфера винаги може да бъде описана близо до пресечен конус. Центърът му лежи на правата O1O2

О – центърът на описаната сфера R – радиусът на описаната сфера, равен на радиуса на описаната окръжност около ΔACD

Топка може да бъде вписана в пресечен конус тогава и само тогава, когато образуващата е равна на сумата от радиусите на основите L=R+r => има вписана топка.

VI Повърхностна площ на пресечен конус

1. Нека P е върхът на конуса, от който се получава пресеченият конус, AA1 е една от образуващите

Пресечен конус O и O1 - центровете на основите. Използвайки формулата Sside за конус, получаваме

S страна \u003d πr * PA-πr1*PA1=πr(PA1+AA1)- πr1PA1, следователно, като вземем предвид, че AA1=L, намираме

Sстрана =πrL +π (r - r1)PA1

Ние изразяваме PA1 по отношение на L1, r и r1. Правоъгълните триъгълници RO1A1 и ROA са подобни, защото имат общ остър ъгъл P и следователно PA1/PA=r/r1 или PA1/PA1+L=r/R1. Получаваме PA1=Lr1/R-r1. S=πrL + (π(r-r1)Lr1)/r-r1=πrL+πr1L=πL(r+r1)

2. Площта на пълната повърхност на пресечения конус е равна на сумата от площите на страничната повърхност на пресечения конус и основите

Пълен = S1+S2+Sside=πL(r+r1)+ πR²+πr²

VII Том с пресечен конус

Обемът на пресечен конус V, чиято височина е равна на h, и площите на основите S и S1 се изчислява по формулата