Законите на Кеплер

В света на атомите и елементарните частици гравитационните сили са незначителни в сравнение с други видове силови взаимодействия между частиците. Много е трудно да се наблюдава гравитационното взаимодействие между различните тела около нас, дори ако техните маси са много хиляди килограми. Въпреки това, гравитацията е тази, която определя поведението на "големите" обекти, като планети, комети и звезди, тя е тази, която ни държи всички на Земята.

Гравитацията контролира движението на планетите в Слънчевата система. Без него планетите, съставляващи Слънчевата система, биха се разпръснали в различни посоки и биха се изгубили в необятните простори на световното пространство.

Моделите на движението на планетите привличат вниманието на хората от дълго време. Изследването на движението на планетите и структурата на Слънчевата система доведе до създаването на теорията за гравитацията - откриването на закона за всемирното притегляне.

От гледна точка на земен наблюдател планетите се движат по много сложни траектории (фиг. 1.24.1). Първият опит за създаване на модел на Вселената е направен от Птолемей (

140). В центъра на Вселената Птолемей постави Земята, около която планетите и звездите се движеха в големи и малки кръгове, като в хоро.

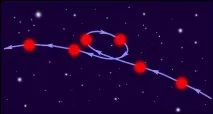Фигура 1.24.1.

Геоцентричната система на Птолемей продължи повече от 14 века и беше заменена от хелиоцентричната система на Коперник едва в средата на 16 век. В системата на Коперник траекториите на планетите се оказаха по-прости. В началото на 17 век немският астроном Й. Кеплер, базирайки се на системата на Коперник, формулира три емпирични закона за движението на планетите от Слънчевата система. Кеплер използва резултатите от наблюденията на движението на планетите от датския астроном Т. Брахе.

Първи закон на Кеплер (1609):

Всички планети се движателиптични орбити със Слънцето в един от фокусите.

На фиг. 1.24.2 показва елиптичната орбита на планетата, чиято маса е много по-малка от масата на Слънцето. Слънцето е в един от фокусите на елипсата. Най-близката до Слънцето точка на траекторията се нарича перихелий, а най-отдалечената от Слънцето точка се нарича афелий. Разстоянието между афелия и перихелия е голямата ос на елипсата.

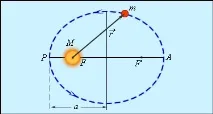Фигура 1.24.2.

Почти всички планети на Слънчевата система (с изключение на Плутон) се движат по орбити, близки до кръговите.

Втори закон на Кеплер (1609):

Радиус векторът на планетата описва равни площи за равни интервали от време.

Ориз. 1.24.3 илюстрира 2-рия закон на Кеплер.

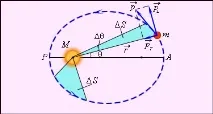Фигура 1.24.3.

Вторият закон на Кеплер е еквивалентен на закона за запазване на ъгловия момент. На фиг. 1.24.3 показва вектора на импулса на тялото и неговите компоненти и Площта, пометена от радиус вектора за кратко време, е приблизително равна на площта на триъгълник с основа и височина:

Тук е ъгловата скорост (виж §1.6).

Ъгловият момент по абсолютна стойност е равен на произведението на модулите на векторите и

защото

От тези отношения следва:

Следователно, ако според втория закон на Кеплер ъгловият импулс по време на движение остава непроменен.

По-специално, тъй като скоростите на планетата в перихелий и афелий са насочени перпендикулярно на радиус-векторите и от закона за запазване на ъгловия импулс следва:

.

Трети закон на Кеплер (1619):

Квадратите на периодите на въртене на планетите са свързани като кубовете на големите полуоси на техните орбити:

или

Третият закон на Кеплер важи за всички планети в Слънчевата система с точност, по-добра от .

На фиг. 1.24.4 показва две орбити, едната от които е кръгла с радиус , а другата е елипсовидна с голям . Третият закон гласи, че ако , тогава периодите на въртене на телата в тези орбити са еднакви.

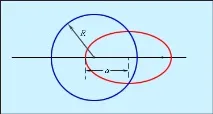Фигура 1.24.4.

Въпреки факта, че законите на Кеплер са най-важната стъпка в разбирането на движението на планетите, те все още остават само емпирични правила, извлечени от астрономически наблюдения. Законите на Кеплер се нуждаеха от теоретична обосновка. Решителната стъпка в тази посока е направена от Исак Нютон, който открива закона за всемирното притегляне през 1682 г.:

където и са масите на Слънцето и планетата, е разстоянието между тях, е гравитационната константа. Нютон е първият, който предполага, че гравитационните сили определят не само движението на планетите от Слънчевата система; те действат между всякакви тела на Вселената. По-специално, вече беше казано, че силата на гравитацията, действаща върху тела в близост до повърхността на Земята, има гравитационен характер.

За кръгови орбити първият и вторият закон на Кеплер се изпълняват автоматично, а третият закон гласи, че , където е периодът на въртене, е радиусът на орбитата. От тук е възможно да се получи зависимостта на гравитационната сила от разстоянието. Когато планетата се движи по кръгова траектория, върху нея действа сила, която възниква поради гравитационното взаимодействие на планетата и Слънцето:

Ако , тогава

Свойството консерватизъм на гравитационните сили (виж §1.10) ни позволява да въведем концепцията за потенциална енергия. За силите на универсалната гравитация е удобно потенциалната енергия да се брои от безкрайно отдалечена точка.

Потенциалната енергия на тяло с маса, намиращо се на разстояние от неподвижно тяло с маса, е равна на работата на гравитационните сили при преместване на масата от дадена точка до безкрайност.

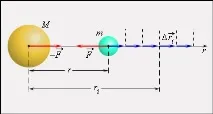
Математическата процедура за изчисляване на потенциалната енергия на тяло в гравитационно поле се състои в сумиране на работата, извършена върху малки премествания (фиг. 1.24.5).

Фигура 1.24.5.

Законът за всемирното притегляне се прилага не само за изсечени маси, но и за сферично симетрични тела. Работата на гравитационната сила върху малко преместване е:

Общата работа при преместване на тяло с маса от първоначалното положение до безкрайност се намира чрез сумиране на работата върху малки премествания:

В границата при , тази сума става интеграл. В резултат на изчисленията за потенциалната енергия, изразът

Знакът минус показва, че гравитационните сили са сили на привличане.

Ако едно тяло е в гравитационно поле на известно разстояние от центъра на тежестта и има някаква скорост, неговата обща механична енергия е

В съответствие със закона за запазване на енергията общата енергия на тялото в гравитационно поле остава непроменена.

Общата енергия може да бъде положителна и отрицателна, а също и равна на нула. Знакът на общата енергия определя характера на движението на небесното тяло (фиг. 1.24.6).

Когато тялото не може да се отдалечи от центъра на тежестта на разстояние. В този случай небесното тяло се движи по елиптична орбита (планети от Слънчевата система, комети).

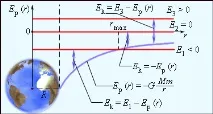Фигура 1.24.6.

Когато тялото може да се оттегли вбезкрайност. Скоростта на тялото в безкрайност ще бъде нула. Тялото се движи по параболична траектория.

Когато движението се извършва по хиперболична траектория. Тялото се отдалечава до безкрайност, имайки запас от кинетична енергия.

Законите на Кеплер важат не само за движението на планетите и другите небесни тела в Слънчевата система, но и за движението на изкуствените спътници на Земята и космическите кораби. В този случай центърът на тежестта е Земята.

Първата космическа скорост е скоростта на спътника в кръгова орбита близо до повърхността на Земята.

оттук

Втората космическа скорост е минималната скорост, която трябва да се съобщи на космическия кораб близо до повърхността на Земята, така че след преодоляване на земната гравитация да се превърне в изкуствен спътник на Слънцето (изкуствена планета). В този случай корабът ще се отдалечи от Земята по параболична траектория.

оттук

Ориз. 1.24.7 илюстрира космическите скорости. Ако скоростта на космическия кораб е равна и насочена успоредно на повърхността на Земята, тогава космическият кораб ще се движи по кръгова орбита на малка височина над Земята. При начални скорости по-големи от, но по-малки от , орбитата на кораба ще бъде елипсовидна. При начална скорост корабът ще се движи по парабола, а при още по-висока начална скорост по хипербола.

---