Значението на МЕТОДА НА ГОЛЕМИТЕ ЧАСТИЦИ в математическата енциклопедия
Значение на МЕТОДА НА ГОЛЕМИ ЧАСТИЦИ в математическата енциклопедия:
- метод за изчисляване на свиваеми потоци на непрекъсната среда [1]. K.h.m. се основава на разделянето на оригиналната система от диференциални уравнения на физически процеси (виж [3]). Той решава еволюционната система от уравнения. В резултат на установяването се допуска стационарно решение. К. ч. м. е развитие на метода на Харлоу "частици в клетките". К. ч. м. се използва широко за изследване на аерогазодинамиката. потоци, дифракционни проблеми, трансзвукови потоци, явления на взаимодействие на радиация с материя и др.
Различната схема на K. h. m. може да бъде описана с помощта на примера за движение на идеален свиваем газ (уравненията на непрекъснатостта, импулса и енергията):
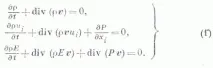
Тук - време, - плътност, = - скорост,E -обща специфична енергия,P -налягане. За затваряне на системата (1) се използва уравнението на състоянието
- вътрешна специфична енергия.
Процесът на решаване на еволюционната система (1) е разделен на времеви стъпки, всяка от които се състои от три етапа: Ойлер, Лагранж и финал. Първо се разглежда промяна във вътрешното състояние на подсистема - "голяма частица" (етап на Ойлер), а след това - изместване на тази подсистема без промяна на вътрешното състояние (лагранжиан и крайни етапи).
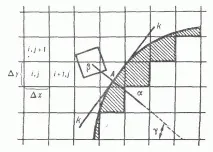
Етап на Ойлер. Областта на интегриране е покрита от фиксирана (Ойлерова) диференциална решетка с произволна форма [за краткост се разглежда правоъгълна решетка в двумерна (плоска) област (виж Фиг.)]. На този етап от изчислението се променят само количествата, свързани с клетката като цяло, и се приема, че течността е забавена за момент.
Следователно, конвективните условия на формата, съответстващи на ефектитепреместванията от уравнения (1) са пропуснати. В останалите уравнения (1) е извадено от диференциалния знак и уравнения (1) са разрешени по отношение на времевите производни наu, v, E:
Най-простото приближение на крайната разлика (централни разлики) води до следните изрази:

Тук стойностите с дробни индекси се отнасят за границите на клетката, напр.
са междинни стойности на параметрите на потока, получени при предположението, че полето p е "замразено" на слоя. The stability of the Euler stage can be achieved, for example, by introducing elementsof the integral relations of the method into it.In this case, the approximation of the sub-integral functions is carried out in the direction parallel to the axis of the body (see Fig.), i.e., as in the scheme i of the method of integral relations: the initial system of equations is taken in integral form, integrals are approximated in it
Лагранжов стадий. На този етап има масови потоци през границите на клетката. В този случай се приема, че масата на голяма частица се пренася само поради компонента на скоростта, нормален към границата. Така например
и т. н. Знакът определя параметрите и другите граници на клетката. Изборът на тези величини е важен, тъй като силно влияе върху стабилността и точността на изчислението. Възможни са различни представяния на разликата за различни порядъци на точност, със и без оглед на посоката на потока, централните разлики, ZIP приближенията и т.н. Импулсните (енергийни) потоци са равни на произведението на съответните стойности на скоростта (обща специфична енергия). Бяха извършени и приближения не само за масовите потоци, но и за импулсните и енергийните потоци.
Крайният етап.На този етап се намират крайните полета на параметрите на потока на Ойлер в момента.Уравненията на този етап са законите за запазване на масатаM,импулса и пълната енергия E, записани за дадена клетка (голяма частица) в разностна форма
M n+1=
Крайните стойности на параметрите на потока на следващия времеви слой се изчисляват по формулите (потокът тече отляво надясно и отдолу нагоре):

Консерватизмът и пълната дивергенция на диференциалната схема (дивергентно-консервативна схема) осигурява уравнението за общата енергияЕ.На последния етап (в случай на използване на дискретен модел на средата) е препоръчително да се извърши допълнително преизчисляване на плътността, което изглажда флуктуациите и подобрява точността на изчисленията. Комбинирайки различни представяния на етапите, се получава серия от различни схеми за CCM, което прави възможно провеждането на широк клас числени експерименти.
K. h.m. позволява тълкуване от различни гледни точки: методът на разделяне, смесеният метод на Ойлер-Лагранж, изчислението в локално лагранжови координати (стадий на Ойлер) с преизчисляване към предишната мрежа (лагранжиан и крайни етапи), записът на разликата в законите за запазване на флуидния елемент - "голямата частица", диференциалната схема на Ойлер.
Граничните условия се задават с помощта на редове от фиктивни клетки (за да се направи всяка изчислителна точка вътрешна и да се поддържа един алгоритъм за всички клетки). За схемата от 1-ви ред на приближение е достатъчен един слой, за 2-ри ред - два слоя и т.н. Нека, например, да разгледаме проблема за изчисляване на потока около осесиметрични и плоски тела с генератор с произволна форма (виж фиг.). Дадените по-рано формули за изчисление са валидни за вътрешните клетки на полето, заобиколени от всички страни с течност, и заклетки, съседни на твърдо тяло, чийто контур съвпада с границите на клетките.
При изчисляване на обтичането на тела по методите на крайните разлики могат да се използват два подхода: изчисляване в координати s, u; въведение в разглеждането на фракционните клетки (виж [2]). В първия случай е трудно да се изчислят тела с прекъсвания и вдлъбнатини. Вторият подход е свободен от тези недостатъци.
Граничните условия върху тялото при дробните клетки се задават, както и при целите клетки, чрез въвеждане на фиктивни клетки. Вътре в тялото се образува слой от фиктивни клетки в съседство с фракционните клетки. За определяне на газовите параметри в тези фиктивни клетки се спуска нормала от центъра на фиктивната клетка а към контура на тялото и в точката на тяхното пресичане А се начертава допирателната k-k (виж фиг.). След това в полето на потока се изгражда определена клетка b, симетрична на тази фиктивна клетка a по отношение на допирателната k-k.Параметрите G в клетката се определят чрез „претегляне“, където сумирането се извършва според тези клетки G, част от площта на която се задават условия на нетечащи условия, за всяка фиктивна клетка на задачата на друг ъгъл на наклон на радиуса, пресичащ контура на тялото в точкатаA.при използване на условията за скорост при движение през повърхността на тялото, не се изисква знак) допълнителен параметър на газов параметър във фиктивна клетка и тогава те ще бъдат
Граничните условия за тяло, чийто контур съвпада с границите на клетките, са частен случай на представените тук гранични условия.
За всяка дробна клетка (виж фиг.) трябва да знаете 5 геометрични. характеристики: където - част от обема на фракционна клетка по отношение на обема на пълна клетка - част от площта на страната, отворена за потока течност и т.н.
Поставянето на плътна граница вътре в клетка въвежда две характеристики: измества центъра на масата от геометричния центърът на клетката е по-близо до границата и намалява действителните размери на клетката. Когато се разглеждат както цели, така и дробни клетки, всички параметри на потока се отнасят до центъра на масата. Именно между центровете на масата се извършва газодинамичната интерполация. функции. В случай на цели клетки центърът на масата или съвпада с геометричния. центъра на клетките (плоска декартова координатна система) или близо до него (цилиндрична координатна система). При реални изчисления разликата дори за ред клетки, съседни на оста, не надвишава , Това обстоятелство не внася значителни изкривявания в резултатите от изчислението. С правилното въвеждане на дробни клетки, изместването на центъра на масата спрямо геометричния. център също не надвишава тази стойност. По-сериозен е проблемът, свързан с намаляването на ефективния размер на клетката. Така че, когато размерът на клетката намалява, условието за стабилност не се нарушава, когато l-xилиy,клетки с са прикрепени към съседни цели числа в потока и получените комплекси се изчисляват с помощта на формулите за дробни клетки. В този случай геометричната размерът на уголемената клетка не е по-малък от размера на цялата клетка: следователно въпросът за стабилността на фракционните клетки отпада.
В равнинния случай геометричният характеристиките на фракционните клетки могат да бъдат получени чрез директно измерване. В осесиметричния случай е необходимо да се извърши допълнително преизчисляване, като се вземе предвид разстоянието на дадена дробна клетка до оста на симетрия. Формулите за разлика за дробни клетки се получават чрез лека промяна на изразите за разлика за цели клетки.
Изследването на диференциалните схеми на C.h.m. (апроксимации, вискозитетни ефекти, стабилност) беше извършено с помощта на диференциални апроксимации (виж [4]). Обобщение е направено от К.
Лит.: [1] Белоцерковски О. М., Давидов Ю. 182-207; [2] Давидов Ю. М., пак там, № 4, стр. 1056-63; [3] Г. И. Марчук, Методи на изчислителната математика, Новосиб., 1973; [4] О. М. Белоцерковски и Ю. М. Давидов, Изследване на схеми на метода на "големите частици" с диференциални приближения, в: Проблеми на приложната математика и механика, Москва, 1971 г., с. 145-55.Ю. М. Давидов.