12. Функцията dEplot3d от пакета dEtools
Функция DEplotSd от пакета DEtools
В редица случаи е удобно да се представи решението на системи от диференциални уравнения под формата на пространствени криви - например линии с еднакво ниво или просто под формата на криви в пространството. Това се прави с помощта на функцията DEplot3d:
DEplot3d(deqns, vars, trarige, initset, o)
DEplot3d(deqns, vars, trang, yrange, xrange, initset, o)
Целта на параметрите на тази функция е подобна на тази, определена за функцията DEplot.
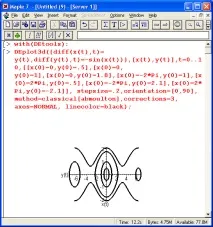
Фигура 13.10 обяснява използването на функцията DEPlqt3d за решаване на система от две диференциални уравнения с изхода на фазовия портрет на трептенията под формата на параметрично определена зависимост x(t), y(t). В този случай фазовият портрет се изгражда върху равнина според вида на конструкцията на графики/линии с еднаква височина.
Друг пример (фиг. 13.11) показва решението на система от две диференциални уравнения с изграждането на триизмерен фазов портрет. В този случай се използва тримерна координатна система и графичните графики съответстват на параметричните зависимости x(t), y(t) и z(t). Появата на фазовия портрет наподобява триизмерна спирала, разгръщаща се в пространството.
Функционалното оцветяване прави графиката пикантна.
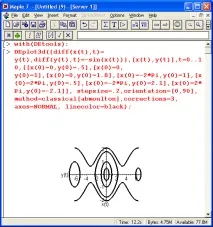
Фиг. 13.10.Пример за решаване на система от две диференциални уравнения с помощта на функцията DEptot3d
Възможностите на функцията DEplot3d ви позволяват да решавате системи, състоящи се от повече от две диференциални уравнения. В този случай обаче броят на решенията, които могат да бъдат представени графично, надхвърля това, което е възможно за триизмерната графика. В същото време зависи от потребителя кои от зависимостите са пропуснати по време на изграждането и кои са изградени.
13. Функцията pdEplot на пакета dEtools.
DEtools PDEplot функция
Друга функция на пакета DEtools еDEtools[PDEp1ot] - използва се за начертаване на решение на системи с квазилинейни частни диференциални уравнения от първи ред в частни производни.
Тази функция се използва в следната форма:
PDEplotCpdiffeq, van, i_curve, srange, o)
PDEplot(pdiffeq, var, i_curve. srange, xrange, yrange, urange, o)
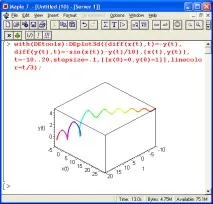
Фиг. 13.11.Пример за решаване на система от две диференциални уравнения с изграждането на триизмерен фазов портрет
Тук, в допълнение към споменатите по-рано параметри, се използват следните: pdiffeq са квазилинейни диференциални уравнения от първи ред (PDE), vans е независима променлива и i_curve са начални условия за параметрични криви на триизмерна повърхност. В допълнение към опциите, посочени за функцията DEplot, тук могат да се използват следните опции:
basechar = TRUE, FALSE. САМО - настройва показването на основните характеристики на кривите;
basecolor, basecolor = b_color - задава цвета на базовите характеристики;
initcolor, initcolor =i_color — инициализация на цвета;
numchar = integer - задава броя на сегментите на кривата, който не трябва да бъде по-малък от 4 (по подразбиране 20);
numsteps = [integerl.integerZ] — задава броя на стъпките на интегриране (по подразбиране [10, 10]).
Фигура 13.12 показва използването на функцията PDEplot. Този пример показва колко необичайно може да бъде решението дори на проста система от частични диференциални уравнения.
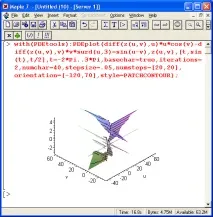
Фиг. 13.12.Пример за PDEplot
В този случай решението е представено от триизмерна фигура с много неправилна форма.
Друг пример за използване на функцията PDEplot е показан на фиг. 13.13. Той илюстрира комбинираното начертаване на решения от различни типове с помощта на функционалазасенчване, реализирано по зададена формула с помощта на опцията initcolor.
Още веднъж отбелязваме, че за съжаление фигурите в тази книга не дават представа за цвета на показаната графика на Maple. Следователно видимостта на решенията, видими на екрана на монитора, е значително по-висока.