1.2. Проекционен метод
В дескриптивната геометрияпроекционният методсе използва за показване на геометрични изображения в равнина. Подпроекцияразберете геометричните конструкции, които трябва да бъдат
завърши, за да получитепроекциятана геометричното изображение. Изучаването на метода на проекцията започва с изграждането на точкови проекции, тъй като всяка геометрична фигура трябва да се разглежда като набор от всички точки, принадлежащи към нея. Има:централнииуспореднипроекции.
1.2.1. Каква е същността на централната проекция?
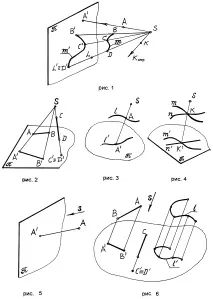
Централнатапроекция е най-разпространеният начин за получаване на проекции на геометрични изображения. Централният проекционен апарат се състои от проекционния център S и равнината , наречена проекционна равнина (фиг. 1.). За да се получи централната проекция на точка А, е необходимо да се начертае проектиращият лъч SA до пресичането му с проекционната равнина . A е централната проекция на точка A върху равнината .
Ако точка K лежи върху проектиращ лъч, успореден на проекционната равнина, тогава нейната централна проекция ще бъде неправилна точка K.
Ако две или повече точки лежат на един и същ проектиращ лъч, тогава те се наричат конкуриращи се(фиг. 1, точки D и L).
За да се получи централната проекция на линия, е необходимо да се проектира набор от точки от тази линия върху проекционната равнина (фиг. 1, крива m). Централната проекция се използва при изграждането на перспективни чертежи на сгради, конструкции и в живописта. Централните проекции са много ясни.
Обърнете внимание на свойствата на проекциите под централната проекция:
1. Проекцията на точка е точка.
2. Проекцията на права е праваПроекцията на права е в общия случай права (фиг. 2, права AB). Ако линията е същата като посоката на проекцията,тогава неговата проекция е точка (фиг. 2, линия CD).
3. Ако една точка принадлежи на права, то проекцията на тази точка принадлежи на проекцията на правата(фиг. 3).
4. Пресечната точка на линиите се проектира в пресечната точка на проекциите на тези линии(фиг. 4).
Тези свойства са очевидни и произтичат от самия метод на конструиране на проекции.
1.2.2. Каква е същността на паралелната проекция? Какви са свойствата на паралелните проекции?
Ако центърът на проекциите S в централната проекция се отстрани до безкрайност, тогава проектиращите лъчи могат да се считат за успоредни. Следователно паралелният проекционен апарат се състои от проекционната равнина и проекционната посока s. Ако през точка А (фиг. 5) се прекара проектираща греда, успоредна на направлението s, то пресичайки проекционната равнина , тя ще даде успоредна проекция А на точка А.
Свойствата на проекциите за централна проекция са валидни и за успоредни проекции (фиг. 6). Паралелните проекции обаче имат и други свойства. Те включват следните свойства:
1. Проекциите на успоредни прави са успоредни.
Наистина, от фиг. 7 се вижда, че правите AA, BB и CC, DD образуват две успоредни равнини. Пресичайки се с третата равнина , те дават успоредни прави ABи CD.
2. Ако отсечка е разделена на точка в някакво съотношение, тогава проекциите на отсечката се разделят на проекцията на тази точка в същото съотношение.
На фиг. 8 са дадени права отсечка AB и разделяща я точка C спрямо AC / CB. След като начертаем AC1AСи CB1СВ, ще получим два подобни триъгълника –ACC1СВВ1. От тяхното сходство следва пропорционалността на страните:
следователно AC / CB=AC/ CB.
3. Плоска фигура, успоредна на равнината на проекциите, се проектира върху тази равнина безизкривяване.
Паралелната проекция, за разлика от централната, осигурява лекота на конструиране и по-голяма връзка с оригинала. Този тип проекция се използва за конструиране на визуални (аксонометрични) изображения на геометрични фигури.
Специален случай на паралелна проекция, при която проекционната посока е перпендикулярна на проекционната равнина
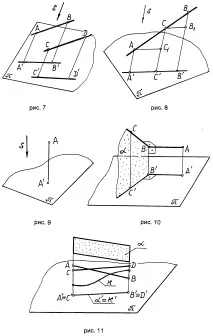
йони (s) се наричаортогоналенилиправоъгълен(в друг случай -наклонен). Ориз. 9 дава визуално представяне на ортогоналната проекция: A е ортогоналната проекция на точка A върху проекционната равнина.
Наред със свойствата на паралелните проекции, следното свойство е валидно за ортогоналните проекции:
Ако поне едната страна на прав ъгъл е успоредна на проекционната равнина, а другата страна не е перпендикулярна на нея, тогава правият ъгъл се проектира върху тази проекционна равнина без изкривяване.
На фиг. 10 е зададен ъгъл ABC = 90; страна AB и страна BC. Нека докажем, че ABC= 90. Страна AB, като тя е перпендикулярна на две пресичащи се прави от тази равнина (ABBC по условие и ABBB по построение). Но ABAB, следователно, AB, и следователно ABBC, т.е. ABC = 90.
Ортогоналните проекции са по-опростени като очертания, лесни за измерване и затова са най-широко използвани в техническото чертане.
Разгледаните методи позволяват решаването на директния проблем на дескриптивната геометрия, т.е. изградете плосък чертеж от оригинала. За да се реши обратната задача, е необходимо да се възстанови формата, размерите на оригинала, местоположението му в пространството от плоско изображение. Проекцията върху една равнина не дава пълна картина на оригинала, както се вижда от фиг. 11. Правата ABе проекция не само на правата AB, но и на правата CD, както и кривата k иравнина лежаща в равнината на проекцията.
За да бъде чертежът обратим, той трябва да бъде допълнен по определен начин. В дескриптивната геометрия се използват много различни методи за получаване на обратими проекционни чертежи. Такива чертежи включват сложен чертеж, перспективен чертеж, чертеж с цифрови знаци и др. Комплексните чертежи са получили най-голямо приложение в техническото чертане.