1.2. Уравнения на геометричните отношения
Както преди, началото на координатите е поставено в точката, оста е насочена надясно, оста е нагоре.
, ,,,
, ,.
Последните две отношения се получават чрез интегриране на равенствата
И.
2.Определяне на ъгловата скорост и ъгловото ускорение на маховика.
2.1. Кинетична енергия на системата
Кинетичната енергия на механизма се намира като сума от кинетичните енергии на неговите връзки
.
Кинетична енергия на въртящ се маховик:
,
е инерционният момент на маховика около оста на въртене.
Кинетична енергия на прогресивно движещ се зад кулисите:
,
Кинетична енергия на ролка, движеща се в равнина:
,
- инерционният момент на ролката около оста, минаваща през нейния център на масата.
Кинетична енергия на системата:
.
След идентични трансформации:
- инерционният момент, намален към водещата връзка.
2.2. Производна по време на кинетичната енергия
Производната по време на кинетичната енергия се намира по правилото за изчисляване на производната на произведението и производната на сложна функция
.
2.3. Елементарна работа и мощност на външните сили и работата на външните сили върху крайното преместване(механизъм в хоризонталната равнина)
В случай, че механизмът е разположен в хоризонтална равнина, само въртящият момент върши работата. Тогава елементарната работа се определя от равенството
.
Работа при завъртане на маховика под ъгъл
.
2.4. Определяне на ъгловата скорост на маховика, когато се завърти на ъгъл φ*
За да определим ъгловата скорост на маховика, прилагаме теоремата за промяната на кинетичната енергия в крайната форма, като приемем, че механизмът е бил в покой в началния момент.
, ,.
Заместването в това равенство на намерени изрази дава
,
където.
.
2.5. Определяне на ъгловото ускорение на маховика, когато се завърти на ъгъл φ*
Използваме теоремата за промяната на кинетичната енергия в диференциална форма
, .
Замествайки стойностите, намерени по-горе, в това уравнение, намираме
.
(1)
Товадиференциално уравнение от втори редописва движението на кобиличния механизъм. Може да се интегрира само числено и също да се използва за намиране на ъгловото ускорение на маховика в неговата произволна позиция.
Нека определим ъгловото ускорение на маховика при неговия ъгъл на въртене.
.
3. Дефиниция на сили
3.1. Определяне на реакциите на лагера и крилата в положениеφ*
Нека определим реакцията на лагера върху оста на маховика и силата, която задвижва връзката, като използваме принципа на д'Аламбер, като разглеждаме движението на маховика отделно от другите тела на системата.
Маховикът се върти. Външни сили, освен двойка сили с момент, действат върху него с реакцията на лагера и реакцията на крилата (фиг. 3). Системата от инерционни сили се свежда до двойка с момент, насочен срещу въртене, тъй като тя се ускорява (фиг. 3).
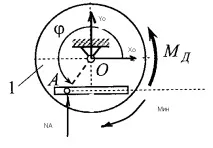
Записване на условието за равновесие за плоска система от външни сили
.
Под ъгъл
3.2. Определяне на силата, която задвижва сцената
Силата, която привежда в движение сцената, според третия закон на динамиката е равна на реакцията на сцената и е насочена в обратна посока.
, rad/s
, rad/s2
,
, Н
,
Министерство на образованието и науката на България
Федерална държавна автономна образователна институция за висше професионално образование „Уралски федерален университет
на името на първия президент на БългарияБ. Н. Елцин