2. Етапи на решаване на конструктивния проблем
Решаването на строителен проблем обикновено включва четири стъпки:
анализ, изграждане, доказване и изследване. Нека разгледаме всеки от тях поотделно.
1. Анализ.На този етап се извършва търсене на решение на проблема. Неговата крайна цел е да установи последователност, алгоритъм, състоящ се от основни или елементарни конструкции, водещи до изграждането на желаната фигура. Освен решаването на геометрична задача за изчисление и доказателство, търсенето на такъв алгоритъм е придружено с чертеж, илюстрация, която помага да се установят връзки и зависимости между данните и желаните фигури.
2. Конструиране.Този етап от решението е директно внедряване на намерения алгоритъм върху чертежа с помощта на избраните инструменти за конструиране.
3. Доказателство.Целта му е да докаже, че фигурата, построена на предишния етап, наистина е желаната, т.е. отговаря на всички условия, поставени в задачата.
4. Проучване.Този етап от решението се състои в установяване дали проблемът винаги има решение; ако не винаги, то при какви конкретни данни и точно колко решения има. В същото време решенията се считат за различни, ако дават неравни фигури (или ако са равни, тогава те са различно разположени спрямо фигурата, с която е свързана конструкцията).
Ние илюстрираме тези стъпки с конкретен пример.
Задача. Построете успоредник по основаа,височинаhи един от диагоналитеd.
Според условието данните са сегменти, представляващи основата, височината и диагонала на успоредника (фиг.). Всички тези фигури се считат за вече изградени и следователно не е необходимо обяснение.
1.Анализ. Нека направим илюстрация, като приемем, че необходимият успоредникABCDвече епостроен (фиг.). Маркираме тези елементи на чертежа:
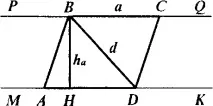
Установяваме връзки и зависимости между елементите на успоредника. Забелязваме, че противоположните страниABиDCлежат на успоредни прави, разстоянието между които е равно на височинатаh. Следователно можете да построите триъгълникABDи след това да го завършите до успоредникABCD.Получаваме следния алгоритъм за построяване на желаната фигура:
1) Построяваме успоредни правиMKиРQна разстояниеhедна от друга.
2) На праватаMKотделете отсечкатаAD=а.
3) От точкатаD,като от центъра, с радиусd, начертайте окръжност и намерете точкатаBна нейното пресичане с праватаPQ.
4) На лъчаВQотделете отсечкатаBC = a.
2.Строителство. Всички етапи от алгоритъма за конструиране се изпълняват с пергел и линийка директно върху чертежа, като се използват посочените елементи (фиг. 157).
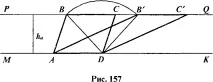
3. Доказателство.Да разгледаме четириъгълникABCD.Неговите противоположни страниADиBCса успоредни, тъй като лежат на успоредни правиMKиPQ.Същите страни са равни по конструкция:
AD=BC=a.И така,ABCD-е успоредник сAD=a, BD=d, а височината еh,тъй като разстоянието между успоредните правиMKиPQеh(по конструкция). Следователно,ABCD-желан успоредник.
4. Изследване.Нека проверим възможността за построяване на успоредникABCDдиректно чрез стъпките на алгоритъма за построяване.
1) Паралелни правиMKиPQна разстояниеhвинаги могат да бъдатизграждане, и то по уникален начин.
2) Също така винаги е възможно да се построи отсечкаAD=aна праватаMKи освен това по уникален начин.
3) Окръжност, начертана от центъра D с радиусd,ще има общи точки с праватаPQсамо когатоd≥h. Акоd=h, тогава получавате една обща точкаB,акоd>h,тогава две общи точкиBиB'.
5) Тези конструкции винаги са уникално осъществими. Следователно решението е възможно, акоd≥h. Акоd=h, тогава проблемът има уникално решение, акоd>h, тогава има две решения.