20-22 билет
20. Координатицентрове на тежестта на еднородни тела. Начини за определянето им.
За хомогенно тяло теглотоphна която и да е част от него е пропорционално на обемаυhна тази част:pk=γυk,и теглотоPна цялото тяло е пропорционално на обемаVна това тяло, т.е.P=γV,къдетоγ— тегло на единица обем.
Положението на центъра на тежестта на хомогенно тяло зависи само от неговата геометрична форма и не зависи от стойносттаγ. По тази причина точкатаС,чиито координати се определят по формули, се наричацентър на тежестта на обемаV.
Чрез аналогични разсъждения е лесно да се установи, че ако тялото е хомогенна плоска и тънка плоча, тогава за него.
къдетоSе площта на цялата плоча;skса площите на неговите части.
Точката, чиито координати се определят по формули, се наричацентър на тежестта на областтаS.
По същия начин се получават формули за координатитена центъра на тежестта на правата:
къдетоLе дължината на цялата линия;lkса дължините на неговите части.
Центърът на тежестта на едно хомогенно тяло се определя като център на тежестта на съответния обем, площ или линия.
Центърът на тежестта на триъгълниклежи в пресечната точка на неговите медиани.
Център на тежестта на дъгата. Кръгове.
Симетрия.Ако едно хомогенно тяло има равнина, ос или център на симетрия, тогава неговият център на тежестта лежи съответно или в равнината на симетрия, или върху оста на симетрия, или в центъра на симетрия.
Разлагане.Ако едно тяло може да бъде разделено на краен брой такива части, за всяка от които е известно положението на центъра на тежестта, тогава координатите на центъра на тежестта на цялото тяло могат да бъдат директно изчислени с помощта на формули. ПриВ този случай броят на членовете във всяка от сумите ще бъде равен на броя на частите, на които е разделено тялото.
Добавяне.Този метод е специален случай на метода на разделяне. Прилага се за тела с изрези, ако са известни центровете на тежестта на тялото без изрез и на изреза.
Интегриране.Ако тялото не може да бъде разделено на няколко крайни части, чиито позиции на центровете на тежестта са известни, тогава тялото първо се разделя на произволни малки обеми Δυk, за които формулите (60) приемат формата
къдетоxk,yk,zkса координатите на някаква точка, разположена вътре в обема Δυk.т.е. свиване на тези обеми в точки. Тогава сумите в равенствата се превръщат в интеграли, разширени до целия обем на тялото, а формулите дават границата:
xc = 1/V



По същия начин за, координатите на центровете на тежестта на площи и линии се получават в границите от формулите:
xc = 1/S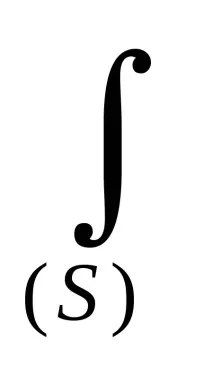
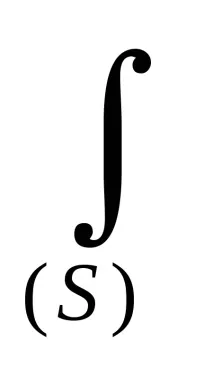
xc = 1/L
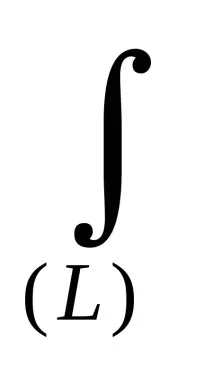
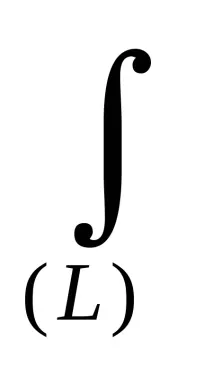
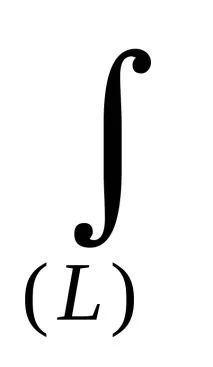
Експериментален метод.Центровете на тежестта на нехомогенни тела със сложна конфигурация (самолет, парен локомотив и др.) могат да се определят експериментално. Един от възможните експериментални методи (метод на окачване) е тялото да бъде окачено на нишка или кабел в различните му точки. Посоката на нишката, на която е окачено тялото, всеки път ще дава посоката на гравитацията. Пресечната точка на тези посокиопределя центъра на тежестта на тялото. Друг възможен начин за експериментално определяне