§ 27. Проблеми на кликата, изоморфно вграждане и изоморфен подграф
Нека G и G' са две графики. Изисква се да се установи дали съществува подграф в графа G', изоморфен на графа G. Този проблем с изоморфен подграф е един от най-трудните алгоритмични проблеми в теорията на графите.
Друг вариант на този проблем е проблемът с изоморфното вграждане: изисква се да се установи дали съществува генериран подграф в G', който е изоморфен на G. Проблемът с изоморфния подграф се превръща в проблем с изоморфизма на графа, ако допълнително зададем \G\ = \G'\ и \EG\ = lEG'l. По подобен начин проблемът за изоморфното вграждане се превръща в проблем за изоморфизма, ако поставим G = G'.
Проблемът с кликата често се разглежда в следната форма: дадена е графика G и естествено число c; установи дали неравенството phi (G)c е вярно
Очевидно проблемът с кликата е специален случай както на проблема с изоморфния подграф, така и на проблема с изоморфната вграденост: необходимо е да се установи дали пълната графа Kc е подграф на графа G. Всъщност тези три проблема са еквивалентни, т.е. както проблемът с изоморфната вграденост, така и проблемът с изоморфния подграф могат да се разглеждат на свой ред като специални случаи на проблема с кликата. Този факт е доказан за първи път от G. Vizing, използвайки неговата конструкция на модулен продукт от графики. По-удобно е да се разглежда не самият продукт Vizing, а допълнителна графика към него, именно тази конструкция се нарича модулен чертеж по-долу.
Модулният продукт G>G' на графиките G и G' е граф, определен от следните условия:
V(G <> G'> = VGx VG' е декартовото произведение на множествата VG и VG'
върховете (u, u'] и (v, v') на G<G' са съседни тогава и само ако и двете v, u' v'
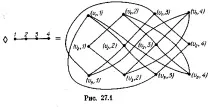
uv EG, uv' EG' или uv EG, u'v' EG' Фиг. 27.1).
Теорема27.1(V. G. Vizing, 1975).Граф G е изоморфно вграден в граф G' тогава и само ако γ(G<G')>=G.
► Нека G=n. Нека графиката G' съдържа . роден подграф G, изоморфен на G, ψ VG->
VН е графов изоморфизъм, VG = , ψ(i) = vi= 1, n . От дефиницията на модулния продукт следва директно, че върховете (1, v1), (2, v2), ., (n, vn) са съседни по двойки в графа G<G' и следователно ψ (G<>G')n.
Обратно, нека ψ (G<>G')<>n, C е клика в графиката: G<G', съдържаща точно n върха. Тогава C = ((1, v1), 2, V2). (n,vn)>, а върховете vi (i = l, n) са n-двойки различни. Нека H = G'(v1, v2. vn). Ясно е, че съответствието i->vi е изоморфизъм между графите G и H.
Обърнете внимание, че върховете (i, vi) с равни координати с едно и също име не са съседни, така че γ (G <> G') n.
Следователно неравенството от формулировката на предходната теорема всъщност е равенство.
Нека се обърнем към проблема с изоморфния подграф. Тук трябва леко да променим конструкцията на модулния продукт.
Голямо модулно произведение G G r на графики G и G' е графика, дефинирана от следните условия:
върховете (u, u') и (v, v') на G<G' са съседни тогава и само ако u v, u'v' и или uv EG, u'v EG', или uv EG.
Теорема27.2.Граф G има подграф, изоморфен на G, тогава и само ако γ (G <> G') = G.
Доказателството е подобно на доказателството на предишната теорема.