3. Биномиален модел на Кокс–Рос–Рубинщайн.
Нека първо приемем, че за всяка времева стъпка цената на даден финансов актив може да се увеличи или намали само с определен дял. Ако в момент t цената е равна на S, тогава в момент t + D t тя може или да се покачи до uS, или да падне до dS. Нека приемем, че има кол опция за този актив, която има цена C в момент t. Ако цената на базовия актив се повиши до uS, цената на опцията също ще се увеличи до някаква стойност Сup, а ако цената падне до dS, тя ще намалее до стойността Cdown. Тези паралелни ценови промени са показани на фигурата. Тъй като има точно два варианта за промяна на цената на базовия актив, естествено е този процес да се нарече биномен.
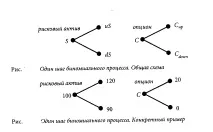
Например, ако S = 100, u = 1,20, d = 0,90, опцията има страйк цена 100 и ще изтече след една времева стъпка. След това, ако цената на активите се повиши до 120, опцията ще струва 20 при упражняване, а ако цената падне до 90, тогава опцията ще се обезцени при упражняване. Този конкретен сценарий е показан на споменатата фигура.
Единствената неизвестна стойност на е C, стойността на кол опцията една стъпка преди упражнението. Ще покажем, че тази стойност може да бъде намерена чрез изграждане на безрисков хедж от опцията и базовите активи.
Помислете за портфолиото, произтичащо от:
а) продажба на три кол опции на цена C всяка,
б) закупуване на две единици дълготрайни активи на цена 100 всяка,
в) заемане на 163,64 за един разглеждан период от време при 10%.
Нетният паричен поток по време на формирането на портфейла ще бъде: 3 С-200 + 163.64 = ЗС-36.36. При изпълнение са възможни два варианта, като всички плащания за всеки от тях са представени в таблицата:
Постъпления от продажба на актив 2 x 120 = 240 2 x 90 = 180
Плащания по къса кол позиция 3 x (-20) = -60 3 x (0) = O
Погасяване на дълг -180 -180
Нетен паричен поток 0 0
Плащания за портфейл, съставен от опции и базови активи
Виждаме, че тази съобразена комбинация от дълготрайни активи, заеми и опции води до едни и същи финансови резултати, когато цената на базовия актив се покачва, докато пада. Така имаме безрисков хедж. Тъй като общата стойност на получения портфейл винаги е равна на нула, неговата справедлива цена по време на формирането също трябва да бъде нула. Следователно, 3C-36.36 = 0 и C = 12.12.
И така, намерихме справедливата цена на опция върху рисков актив за единица време до момента на упражняване. Единствената информация, от която се нуждаем за това, е сумата, с която цената може да се увеличи или намали, както и безрисковия лихвен процент. Изненадващо, не е нужно да знаете вероятностите цената да се повиши или понижи.
Ние илюстрирахме концепцията за хеджиране на безрискова опция с конкретен пример, но самата тази техника е универсална. Като цяло, помислете за портфолио, което включва:
а) продажба на една кол опция,
б) закупуване на h единици дълготрайни активи,
в) заем в размер на Б.
Стойностите на h и B трябва да бъдат избрани така, че финансовият резултат на портфейла при упражняване на опцията да е нула както при увеличение, така и при намаляване на цената на базовите активи. За да направите това, трябва да бъдат изпълнени следните равенства:
където R = eit, i е непрекъснато натрупващият се сложен безрисков лихвен процент,Сupи Cdown са цената на опцията при упражняване в случаи на увеличение и намаление на цената. Резултатът е система от две уравнения с две неизвестни и с помощта на прости алгебрични операции можете да намерите нейните решения:
Равенство на нула на началния потокпари в брой означава това
Замествайки тук изразите за h и B, получаваме:
C \u003d [(R-d) Срр - (u-R) Cнадолу] / R (u-d).
И накрая, след смяната
получаваме малко по-удобен израз за цената на еднопериодна опция:
Стойностите p и (1 - p) изглеждат като вероятности, тъй като техните стойности винаги попадат между нула и едно и полученото съотношение може да се тълкува по следния начин: по всяко време стойността на опцията е равна на текущата стойност на средния краен резултат, ако при изчисляване на средната стойност всеки възможен резултат се взема с тегло, равно на вероятността за неговото възникване.
Нека видим какво дават тези уравнения в конкретния пример, обсъден по-горе:
h = (20 - 0) / (100 (1,20 - 0,90)) = 0,6667, B = (0,90 x 20 - 1,20 x 0) / (1,10 x (1,20 - 0,90)) = 54,55
C =hS- B =0,6667x100 -54,55 =12,12.
Този метод на ценообразуване на еднопериодни опции може лесно да бъде разширен до по-дългосрочни опции. Помислете например за вариант с два периода. На следващата фигура примерът, разгледан по-рано, продължава с още една стъпка. Тук, както и преди, началната цена е 100, u = 1,20, d = 0,90. Ако цената се повиши на всяка от двете стъпки, тогава в крайна сметка тя ще бъде равна на 100 x 1,20 x 1,20 = 144. По същия начин, ако тя пада на всяка стъпка, тогава в крайна сметка ще бъде равна на 81. Ако накрая цената първо се повиши и след това спадне, или обратното, тогава в крайна сметка ще бъде равна на 108.
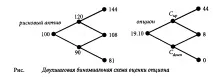
За да оцените опция от две стъпки, можете да разделите целия проблем на няколко по-прости проблема („разделяй и владей“). Нека започнем от горната дясна част на диаграмата на тази фигура и я начертаем отделно на следващата фигура.
P
Горен десен клон
Тази подзадача е по същество същата като задачата с опции в една стъпка. С помощта на съотношения (1) и (2) намираме коефициента на хеджиране h и стойността Сup — те са равни съответно на 1 и 29,09. Правим същото с долната дясна част на разглежданата картина, като същевременно получаваме коефициент на хеджиране от 0,30 и Cdown = 4,85. Намерихме стойността на цената на опцията една стъпка преди упражняване. Остава само да замените получените числа в предишната фигура и да обработите лявата страна на диаграмата - тя е показана отделно на следващата фигура:
P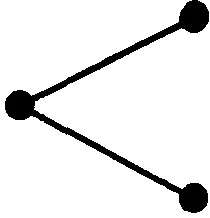
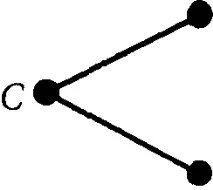
Лявата страна на диаграмата
Това отново е проблем за оценка на опция в една стъпка. Прилагайки отново предишните формули, получаваме коефициент на хеджиране от 0,81 и цена на опция от 19,10. Следващата фигура показва пълната двустепенна верига с всички числени стойности.
Решетката, която описва двустъпковия модел, има три върха, където цената може да се покачва или пада. За всеки от тези върхове, като се използва връзка (1), се определя безрисков хедж от опцията и основния актив. Коефициентът на хеджиране може да се променя от пик до пик. Това е съществено свойство на биномния модел и то отразява реалното! практиката на финансисти, които, когато хеджират портфейл от опции, непрекъснато балансират хеджиращия портфейл, за да поддържат неутрализиране на риска. В примера с две стъпки, показан на последната разгледана фигура, 0,81 от базовия актив ще бъдат взети за хеджиране на опцията. Ако цената на актива след това спадне, тогава 0,51 от базовия актив трябва да се продаде, за да се намали коефициентът на хеджиране до 0,30. Напротив, ако цената на активите се увеличи, трябва да ги купувате в количество0,19, което довежда коефициента на хеджиране до 1.
Точно както разширихме едностъпковия модел до две стъпки, можем да го разширим до произволен брой стъпки. Това ще доведе до "конусовидна" решетка като тези, които разгледахме, но по-дълга. Всеки връх на решетката съответства на цената на базовите активи в даден момент от време. На всяка стъпка цената може да се повишава или пада. Започвайки с текущата пазарна цена в най-лявата точка, мрежата постепенно се разширява, за да покрие всички възможни стойности, които цената на базовите активи може да приеме с течение на времето. Колкото повече време има до упражняването на опцията и колкото по-голяма е променливостта на базовите активи, толкова по-широка ще бъде мрежата.
Числата на възлите на решетката могат да бъдат получени в резултат на следната последователност от действия:
1) Започнете от лявата точка на ценовата мрежа на активите.
2) Попълвайки мрежата отляво надясно, последователно намерете стойностите на цената на основните активи, умножавайки предишните стойности или по и, или по d.
3) За всяка крайна цена на базовите активи намерете стойността на опцията към момента на упражняване.
4) След това попълнете решетката на цената на опцията отдясно наляво, като прилагате връзка (2) всеки път (т.е. модел за ценообразуване на опция в една стъпка).
5) Получената стойност на стойността на опцията в началната точка на мрежата е нейната справедлива цена към момента на сключване на опционния договор.
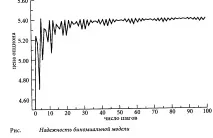
В този пример, използвайки 10-стъпков биномиален модел, можете да откриете, че изискваната справедлива цена на опцията трябва да бъде равна на цената от. Модел Блек-Шоулс. Това предполага, че биномиалният модел изглежда последователен. На практика обаче обикновено се предприемат повече от 10 стъпки, тъй като в противен случай отговорът, даден от биномния модел, няма да бъде напълно надежден.(разбира се, това означава, че в действителност кавичките е малко вероятно да се държат като в биномния модел, но увеличаването на стъпките ви позволява да получите подобно поведение). На следващата фигура са показани резултатите, получени за биномни модели с различен брой стъпки - от 1 до 100. В много комерсиални софтуерни продукти, базирани на този модел, броят на стъпките е от порядъка на 50 - това дава задоволителен компромис между надеждност и време за изчисление.
Биномиалният модел е достатъчно гъвкав, за да работи с базови активи, които се оценяват според дадено разпределение на възвръщаемостта. Желаният закон за промени в цената може да бъде осигурен чрез избор на подходящи стойности за и и d, а в различните части на решетката те могат да бъдат различни. Обикновено u и d се избират така, че биномиалният модел да се доближава до логаритмично нормално разпределение на цените на практика.
Сега ще се опитаме да обосновем предположението, направено в началото на този раздел, че цената на всяка стъпка може да се повишава или пада само със строго определена част. Цялото ни обсъждане на биномния модел се основава на това предположение. На пръв поглед може да изглежда нереалистично, но сега виждаме, че ако стъпките са достатъчно малки и има много от тях, тогава цената може да се промени значително за дълго време. Следователно предположението, направено в началото на този раздел, е съвсем разумно, ако отделните стъпки са малки.
При неограничено увеличаване на броя на стъпките на биномния модел, той съвпада в границата с модела на Black-Scholes. В тази връзка възниква въпросът: защо изобщо е необходимо да се използва биномен модел, свързан с изчислително тромав итеративен процес? Отговорът се крие вче биномиалният модел е приложим с минимални ограничения. Може да се използва за оценяване на опции, за които моделът Black-Scholes е трудно приложим. Например, оценяването на опции от американския тип или опции върху акции с нередовни дивиденти изисква значителна сложност, за да бъде въведена в модела на Black-Scholes. В такива случаи биномиалният модел може да бъде най-простият метод.