42 Производна по посока и градиент

Определение: Градиентът на функцията Z=f(M) в точката M(x; y) е вектор, чиито координати са равни на частните производни в точката M. gradZ=.

Забележка: Използвайки нотацията за градиент, производната на посоката може да бъде записана като:

. Градиентът показва посоката на най-бързия растеж на функцията в дадена точка.

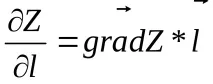
43 Екстремум на функция на две променливи

Нека Z=f(M) е дефинирано в някаква околност на точката M0(x0;y0).

Определение: Функцията Z=f(x;y), има локален максимум/минимум в точката M0, ако има такава близост на точката M0. където за всяка точка M от тази окръжност е в сила неравенството: f(M)f(M0)- максимум / f(M)f(M0)- минимум.

От дефиницията следва, че ако Z има екстремум в точката M0, тогава общото увеличение може да се запише: Z=f(M)-f(M0), Z0- за максимума и Z0- за минимума.

Теоремата е необходимо условие за локален екстремум: Ако Z=f(x;y), има екстремум в точка M0 и в тази точка има частни производни от първи ред, то те са равни на нула.

Документация: фиксираме една от променливите y=y0, след това Z-функцията на една променлива (зависи само от x) и има производна в точката x0 и екстремум в точката x0, след това според необходимото условие за екстремум за функцията на една променлива: ’(x0)=0 => fx'(x0;y0)=0.

Теоремата е достатъчно условие за локален екстремум: Нека функцията Z=f(x;y) има частни производни от втори ред в точка M0 на възможен екстремум и някои от неговите околности. Обозначете: Съставете матрица:

, означете =, след това:

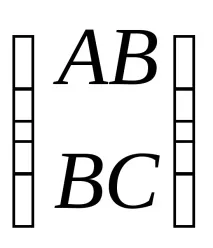
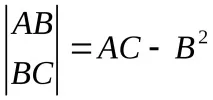
Ако >0, тогава точката M0 е локална точка на екстремум,

Ако  0, A > 0, M0 е минималната точка,

Калкулатор

Услуга за безплатна оценка на цената на работата

1. Попълнете заявление. Експертите ще изчислятцената на вашата работа
2. Изчисляването на цената ще дойде по пощата и SMS

Номерът на вашето приложение

Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.

---