§ 52. Степенно множество на граф

Множеството от мощностина граф е множеството от степени на неговите върхове. Наборът се различава от степенната последователност o по това, че не взема предвид броя на върховете, които имат дадена степен, докато в степенната последователност всяко число се появява толкова пъти, колкото е степента на колко върха е то.

C

означете степенния набор на графикатаGсS(G).Така, за графикатаG,показана на Фиг. 52.1,S(G) == .

Въпреки че степенната последователност на графиката отговаря на определени условия, степенният набор на графиката може да бъде произволен набор. Това се доказва от следното

Теорема 52.1.Всеки краен наборSот естествени числа е степенен набор от някаква прагова графика. Минималният ред на такива графики еs+1,къдетоs—максималния брой от множествотоS.Очевидно тази теорема предполага

Следствие 52.2.Всеки краен набор от цели числа,неотрицателни числа е степенен наборна някаква графика.

Доказателство на теорема 52.1. АкоS(G) ==S,тогава\G\≥s+ 1,, така че трябва само да докажем съществуването на подходяща графикаG.1>. Нека сега

и нека, за определеност,n = 2pе четно число. Ще потърсим желаната графика във формата

къдетоKX°H-​​​​е графиката, получена от графикатаHчрез добавяне наxдоминиращи върхове, аOY°Hе графиката, получена от графикатаHчрез добавяне наyизолирани върхове. Всяка графика от вида (1) е прагова. Нека се опитаме да вземем числатаxaиyβв израз (1), така че равенствотоS(G) =S.

O

очевидно е, че систематаa urот уравнения (2) по отношение на неизвестнитеxi,yj(i=1,p,j=1,p)има решение, всички координати на което са положителни:

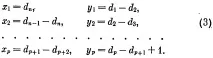
Замествайки в израз (1) числата, определени от равенства (3), получаваме графG,за койтоS(G)=S.Броят на неговите върхове е равен на

За нечетенn = 2p+ 1 конструкцията е подобна, само че вместо формула (1) се използва формулата

---