5.3 Определяне на координатите на точка за свързване на траверс с геодезически мрежи от най-висок клас
Коригиране на ход– това означава получаване на координатите на една точка и дирекционния ъгъл на една линия от хода в една система с контролни точки. Този проблем може да се реши чрез обвързване с ъгъл и гониометричен ход, по метода на директната и резекция, чрез измерване на необходимите ъгли и линии на терена.
ТочкитеMиNса фиксирани точки с известни координати и дирекционен ъгълNM(Фигура 14). При полагане на гониометричен траверсABCDEMелементMсе включва в траверса. За да се изчисли дирекционният ъгъл на първата линия на ходаMA, е необходимо да се измери хоризонталният ъгълNMA =; тогава дирекционният ъгълMAще бъде получен по формулата
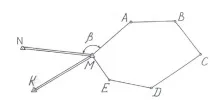
Фигура 14 Ъглово прилепване
За да се получи по-надежден резултат, е необходимо да се получи дирекционният ъгъл на линиятаMAот другата твърда страна, напримерMK. За да направите това, измерете хоризонталния ъгълKMAи изчислете втората стойност на дирекционния ъгълMA. След това се извършва обработката на теодолитния траверс.
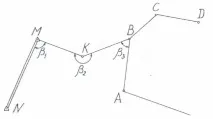
Фигура 15 Свързване чрез щрих
В някои случаи гониометричният траверсABCDе разположен на разстояние от фиксираните точкиM,N(Фигура 15). В този случай се полага допълнителен щрихMKVс измерване на хоризонталните ъглии дължините на линиите. Тъй като координатите на точкатаМи дирекционният ъгъл на праватаМNса известни, е възможно да се изчислят желаните координати на точкатаBи дирекционният ъгъл на праватаBAпоMKVмаршрут по обичайния начин.
1. Каква е целта на дефинирането на допълнителни елементи?
2. В какъв случай е решен проблемът с прехвърлянето на координати от горната част на знака към земята?
3. По коя теорема се изчислява непревземаемото разстояниеAPот триъгълницитеAMPиANP?
4. Какво означава равен ход?
5. Как се извършва ъгловото прихващане?
6. Схема на връзване в движение.
6 Резекция и резекция
6.1 Права кройка (формули на Young)
6.2 Директна резекция (формули на Гаус)
6.3 Резекция (формули на Kneissl)
6.1 Права кройка (формули на Young)
В случаите, когато точките на геодезическата мрежа са разположени на значително разстояние от началото или края на полигонометричния траверс, се използва методът на свързване чрез директен сериф. Задачата е да се намерят координатите на точка от две начални точки и ъглите, измерени в тях. За контрол на правилността на определяне на координатите на точката се използва и трета начална точка. Ъгълът между съседните направления в определената точка трябва да бъде най-малко 30° и не повече от 150°.
Има различни начини за решаване на проблема. Ако има видимост между точкитеAиBи ъглите1и2, които са ъглите на триъгълникаATP(Фигура 16), се измерват при тях, тогаваформите се използват за решаване на проблема uly Young.
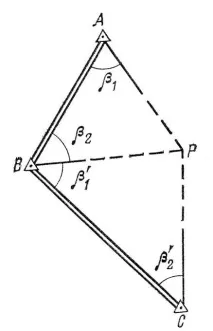
Фигура 16 Прав разрез по формулите на Young
Процедурата за решаване на проблема:
Правило: Ако от началната странаABгледате определяната точкаP, то точкатаAтрябва да е отляво, а точкатаBтрябва да е отдясно.
От триъгълникаATRпо синусовата теорема
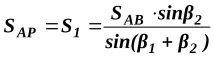
Увеличението на координатите, съответстващи на тази страна, се определя от добре известната формула
(69)
Имайки предвид формула (68) и също
(70)
(71)
От тригонометрията е известно, че
Замествайки тези стойности във формула (71), получаваме
CHAR=(74)
XP - XA = (75)
Разделяйки числителя и знаменателя на дробта на произведението sin 1 sin 2, получаваме:
XP - XA = (76)
По същия начин намираме YР – YА = (77)
Равенствата (76) и (77) са формулите на Юнг за нарастване на координатите.
По същия начин намираме формулите на Young за друга двойка координатни нараствания, съответстващи на разстояниетоВР =S2
XP - XB = (78)
YР – YВ = (79)
Изчисляване на увеличенията на координатите по формули (76) - (79), след което два пъти вземете координатите на точката P
Решавайки уравнения (76) и (77) по отношение наХРиYPи привеждайки десните части до общ знаменател, получаваме формулите на Юнг за координатите
XP=(81)
YP=
Компютърно управление. След като изчислите координатите на точкатаP, можете да вземетеBиPза начални, а точкатаAза определена.
ТогаваXA=(82)
За пълен контрол на правилността на определяне на позицията на точкатаP, имаща координатите на точкитеBиC, определете
XP=(83)
YP=
Несъответствията между координатите, получени при първото и второто решение, трябва да удовлетворяват неравенството
( x - x ) 2 + ( y - y ) 2 3 Mr (84)
където M1 и M2 са UPC на позицията на точка P, определена от две начални точки (A и B; B и C).
M1 =
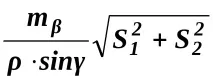
M2 =
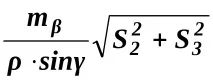
където m - CPC измерване на ъгъл.
За крайните стойности на координатите на точката P се взема средноаритметичното от стойностите, получени с две решения M = Mr / 2.