5.6 Невронна мрежа на Хеминг
Когато е достатъчно да се получи примерният номер на изхода на NN, асоциативната памет се реализира успешно от мрежата на Hamming. Този тип невронна мрежа се характеризира, както може да се види от нейната структура, показана на фиг. 5.4 в сравнение с по-често използваната мрежа на Hopfield, намалявайки разходите за памет и също така намалявайки общото количество изчисления.
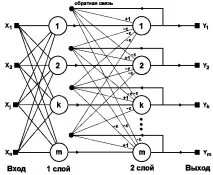
Ориз. 5.4 – Структурата на невронната мрежа на Хеминг.
Идеята зад тази мрежова конфигурация е да се намери разстоянието на Хеминг от тестовата проба до всички проби. В този случай разстоянието на Хеминг се счита за броя на различните битове в два двоични вектора.
Мрежата избира шаблона с минималното разстояние на Хеминг до неизвестния вход, което ще активира само един мрежов изход, съответстващ на този шаблон.
На етапа на инициализация на коефициентите на тегло на първия слой и прага на функцията за активиране се присвояват следните стойности:
wik = 0,5xi k , i = 0. N-1, k = 0, . m-1,
θk = N / 2, k = 0, . m-1,
където xi k е i-тият елемент от k-тата проба, n е броят на характеристиките, m е броят на невроните в слоя.
Коефициентите на тегло на инхибиторните синапси във втория слой се приемат равни на някаква стойност 0 (2 ,j ) = y (1 ,j ) , j = 0, . m-1.
2. Изчислете новите състояния на невроните от втория слой:
и значенията на техните аксони:
.
Функцията за активиране

3. Проверете дали резултатите от невроните на втория слой са се променили през последната итерация. Ако да, преминете към стъпка 2. В противен случай прекратете алгоритъма.
Внимателната оценка на алгоритъма показва, че ролята на първия слой е много условна: използването му веднъж на всекистъпка 1 със стойностите на своите тегловни коефициенти, мрежата вече не се позовава на него, така че първият слой може да бъде напълно изключен от мрежата (заменен с матрица от тегловни коефициенти).
5.7 Машина на Болцман
Машината на Болцман се дава от четворката 0,w>, където N е броят на невроните, E = е наборът от връзки между невроните, i, j= l. В същото време всички автовръзки принадлежат към това множество, тоест подмножество на E. Всеки неврон може да има състояние 0 или 1. Състоянието xk на Болцмановата машина се определя от състоянията на невроните xk= (xk1, . xkN), x0 е първоначалното състояние.