5.6. Скаларен троен продукт
([a, b], c) = (a × b) c.
някаква правоъгълна координатна система, скаларната
продукт се определя по формулата
Доказателство : Извършване на скаларното произведение на векторите
a × b = ( a y b z − a z b y ) i + ( a z b x − a x b x ) j + ( a x b y − a y b x ) k
c = c x i + c y j + c z k
( a × b ) c = ( a y b z − a z b y ) c x + ( a z b x − a x b x ) c y + ( a x b y − a y b x ) c z
a x a y a z = b x b y b z. c x c y c z
Геометрична интерпретация. Абсолютната стойност на числото (a × b) c е обемът на паралелепипед, образуван от векторите a, b и c, както е показано на фигурата по-долу.
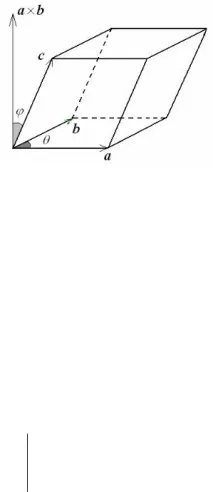
Наистина, обемът на паралелепипеда е равен на произведението от площта на основата и височината.
По теоремата за скаларното произведение,
( a × b ) c = a × b c cos ϕ .
Величината a × b е равна на лицето на успоредника, а произведението c cos ϕ е равно на височината на паралелепипеда.
Следствие 1: Ако три вектора са копланарни, тогава скаларното тройно произведение е равно на нула.
Следствие 2: Четири точки A, B, C и D лежат в една и съща равнина, ако скаларът
тройното произведение ( AB × AC ) AD е равно на нула.
5.6.1. Свойства на скаларното тройно произведение
1) По свойствата на скаларното произведение, a ( b × c ) = ( b × c ) a .
2) С оглед на свойствата на детерминантите,