6.2. Поасоново разпределение
Както вече беше отбелязано, биномното разпределение се доближава до нормалното разпределение приn. Това обаче не се случва, ако заедно с нарастването наnедна от стойноститеpилиqклони към нула. В този случай е валидна асимптотичната формула на Поасон, т.е. приn,p0
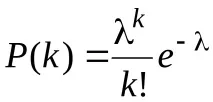
където =np. Тази формула определязакона за разпределение на Поасон, който има самостоятелно значение, а не само като частен случай на биномното разпределение. За разлика от биномното разпределение, тук случайната променливаkможе да приема безкраен брой стойности:k=0,1,2,…
Законът на Поасон описва броя на събитията k, които се случват през равни интервали от време, при условие че събитията се случват независимо едно от друго с постоянна средна интензивност, която се характеризира с параметъра . Полигонът на разпределение на Поасон е показан на фиг. 6.2. Имайте предвид, че за големи dis
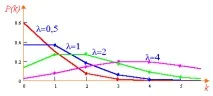
Разпределението на Поасон се доближава до нормалното. Следователно, разпределението на Поасон се използва като правило в случаите, когато има ред на единица, докато броят на опититеnтрябва да бъде голям, а вероятността за възникване на събитиетоpвъв всеки опит е малка. В тази връзка законът на Поасон често се нарича ощезакон за разпределение на редки явления.
Записваме закона на Поасон под формата на таблица
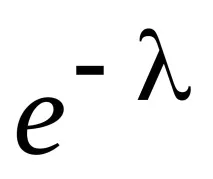
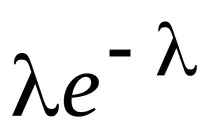
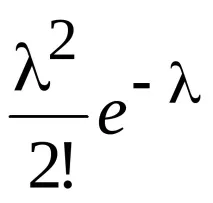
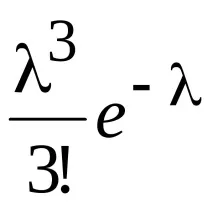
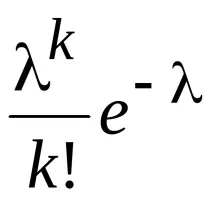
Нека проверим дали сумата от всички вероятности е равна на единица:

Нека намерим числените характеристики на това разпределение. По дефиницията на математическото очакване за DSW имаме
.
Обърнете внимание, че в последната сума сумирането започва отk=1, т.к първият член на сумата, съответстващ наk=0,е равно на нула.
За да намерим дисперсията, първо намираме математическото очакване на квадрата на произволното:
По този начин математическото очакване и дисперсията на случайна променлива, разпределени съгласно закона на Поасон, съвпадат и са равни на параметъра на това разпределение
. (6,8)
Това е отличителната черта на разпределението на Поасон. Така че, ако въз основа на експериментални данни се установи, че математическото очакване и дисперсията на определена стойност са близки една до друга, тогава има основание да се предположи, че тази случайна променлива е разпределена в съответствие със закона на Поасон.
Използвайки концепцията за начален и централен момент, може да се покаже, че за разпределението на Поасон асимметрията и ексцесът са равни:
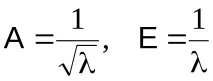
Тъй като параметърът винаги е положителен, разпределението на Поасон винаги има положителна асиметрия и ексцес.
Нека сега покажем, че формулата на Поасон може да се разглежда като математически модел на най-простия поток от събития.
Поток от събитияе поредица от събития, които се случват в произволни моменти. Поток се наричанай-прост, ако има свойстватастационарен,без последействиеиобикновеност.
Интензитетът на потока е средният брой събития, които се появяват за единица време.
Ако константата на интензитета на потока е известна, тогава вероятността за възникване наkсъбития на най-простия поток през времетоtсе определя от формулата на Поасон:
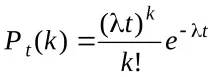
Тази формула отразява всички свойства на най-простия поток. Освен това всеки най-прост поток се описва с формулата на Поасон, така че най-простите потоци често се наричат Поасон.
Свойството на стационарносте товаче вероятността за възникване наkсъбития във всеки интервал от време зависи само от брояkи от продължителносттаtна интервала от време и не зависи от началото на неговото обратно броене. С други думи, ако потокът има свойството на стационарност, тогава вероятността за възникване наkсъбития във времевия интервалtе функция, която зависи само отkи отt.
В случай на най-простия поток, от формулата на Поасон (6.10) следва, че вероятносттаkот събития през времетоt, при даден интензитет, е функция само на два аргумента:kиt, което характеризира свойството на стационарност.
Свойството на липсата на последействиее, че вероятността за възникване наkсъбития във всеки период от време зависи от това дали събитията са се появили или не в моментите от време, предхождащи началото на разглеждания период. С други думи, историята на потока не влияе на вероятностите за събития, настъпили в близко бъдеще.
В случай на най-простия поток, формулата на Поасон (6.10) не използва информация за настъпването на събития преди началото на разглеждания интервал от време, което характеризира свойството за липса на последействие.
Свойството на обикновеносттае, че настъпването на две или повече събития за малък период от време е почти невъзможно. С други думи, вероятността за възникване на повече от едно събитие за малък период от време е незначителна в сравнение с вероятността за възникване само на едно събитие.
Нека покажем, че формулата на Поасон (6.10) отразява свойството ординалност. Поставяйкиk=0 иk=1, намираме съответно вероятностите за липса на събития и за възникване на едно събитие:
Следователно вероятността за възникване на повече от едно събитие е равна на
.
Използване на разлаганефункции
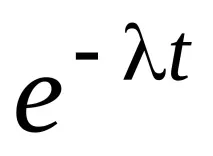
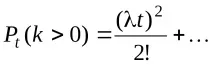
СравнявайкиPt(1) иPt(k>1), заключаваме, че за малки стойности наt, вероятността за поява на повече от едно събитие е пренебрежимо малка в сравнение с вероятността за поява на едно събитие, което характеризира свойството за обикновеност.
Пример 6.2.При наблюденията на Ръдърфорд и Гайгер, радиоактивно вещество е излъчило средно 3,87 -частици за интервал от време от 7,5sec. Намерете вероятността за 1сектова вещество да излъчи поне една частица.
Решение.Както вече отбелязахме, разпределението на броя на -частиците, излъчени от радиоактивен източник за определен период от време, се описва с формулата на Поасон, т.е. формира най-простия поток от събития. Тъй като интензитетът на излъчване на -частици за 1секе равен на
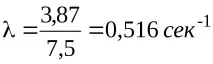
тогава формулата на Поасон (6.10) приема формата
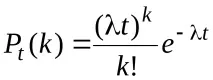
Така вероятността заt=1secвеществото да излъчи поне една частица ще бъде равна на
.