7 Лекция № 6

Продължителност:2 часа (90 мин.)

7.1 Ключови въпроси

7 Лекция № 6. Свойства на бинарните отношения 1

7.1 Ключови въпроси 1

7.2 Текст на лекция 1

7.2.1 Свойства на бинарните отношения 1

7.2.2 Отношения на еквивалентност 5

7.2.3 Отношения от ред 8

7.2.4 Контролни въпроси 12

7.2 Текст на лекцията

7.2.1 Свойства на бинарните отношения

Отношенията се делят на различни видове в зависимост от свойствата, които притежават.

НекаR–е релация в множествотоM,.Тогава:

–ОтношениеRрефлексивноако

, т.е.aRaсе отнася за всяко

(например връзката „живея в същия град“ е рефлексивна).

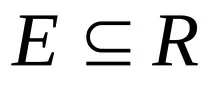
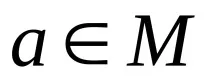
Рефлексивните отношения се представят от матрица, която винаги има такива на главния диагонал. В граф, представляващ рефлексивна релация, всички върхове имат цикли.

–ОтношениеRантирефлексивако, т.е. акоaRaне важи за нито един

(например отношението "да бъдеш син" е антирефлексивно).

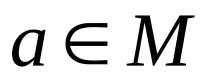
В матрицата на такава връзка има нули на главния диагонал и нито един връх в графиката няма цикли.

–СъотношениеRсиметричноако

, т.е. акоaRbе вярно, тогаваbRaсъщо е вярно (например релацията "учене в същата група" е симетрична).

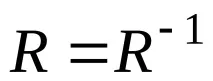
В матрицата на това съотношение елементите, които са симетрично разположени спрямо главния диагонал, са равни помежду си, т.е.

. В симетричната релационна графика за всяка дъга, преминаваща от връхiдо връхj, има дъга назад. Следователно в такава графика е възможно да не се посочи посоката на дъгите и да се представи симетричното отношениекато неориентиранографика.

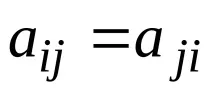
–СъотношениеRасиметричноако

. Това означава, че от двете релацииaRbиbRаза различни елементи, поне една не е изпълнена (например релацията "да си син" е асиметрична).

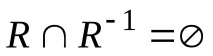
За матрични елементи на такава връзка

е изпълнено и в графиката няма дъги с различни посоки, свързващи два върха.

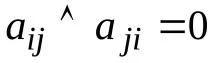
Ако връзката е асиметрична, тогава тя е и антирефлексивна, което означава, че диагоналните елементи на съответната матрица са равни на 0 и в графиката няма цикли.

–ОтношениетоRе антисиметричноако

, което означава, чеaRbиbRамогат да бъдат изпълнени само акоa =b(пример: отношение на равенство, паралелизъм).

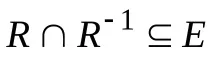
За елементите на матрицата на такава връзка,

Може да има цикли в графиката на тази връзка, но никоя от дъгите няма противоположни дъги.

–ОтношениетоRе транзитивноif

, което означава, че изпълнението наaRbиbRcпредполагаaRc(например релациите "да бъдеш по-голям", "да бъдеш по-млад" са транзитивни).

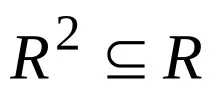
Според дефиницията квадратът на матрицата на такова отношение не трябва да съдържа „допълнителни“ 1s, т.е. тези, които не са били в матрицата на взаимоотношенията.

В графиката на тази връзка, ако всеки два върха са свързани с път с дължина 2, тогава те също трябва да бъдат свързани с дъга, насочена от началото на пътя към неговия край.

Ако релациятаRе транзитивна, тогава нейното транзитивно затваряне е равно на самата нея:R○ =R. Следователно може да се твърди, че акоR=R○ , тогава отношениетоRе транзитивно.

–Rе антитранзитивно, ако за всякоn

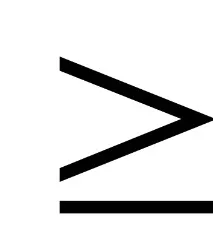
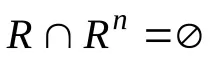
Това означава, че наличието на пряка връзка между елементитеaиbелиминира заобиколни решения.

АкоR–е строг ред (за редове вижте § 7.2.3), тогава редукцията на това отношениеRrе антитранзитивна (вижте фиг. 8.15 за пример).

Всяка антипреходна връзка е асиметрична и следователно антирефлексивна. Графиката на такава връзка няма контури, включително контури и паралелни пътища.

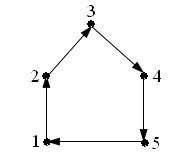
За отношениетоR(фиг. 7.1), чиято графика е контур, получаваме

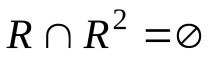
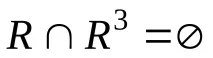
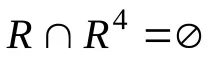
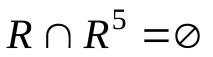
и можете да мислите за него като за антипреходно, но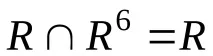

, така че това отношение не е антипреходно.

Като цяло, за отношенияRпод формата на контур

Фигура 7.1 - Графика на неантитранзитивна връзка

От особен интерес е въпросът за зависимостта на свойството на резултата от операцията от свойствата на отношенията, включени в операцията.

Отговорът на този въпрос е даден в таблица 7.1. При двоичните операции и двата операнда (освен ако не е посочено друго) трябва да имат съответното свойство.