9.4. Концепцията за паралелно изчисление
Моделът на машината на Тюринг предполага последователно изпълнение на елементарни операции. Такъв модел съответства на понякога използвания модел "единичен калкулатор", който има ниска изчислителна скорост в техническата си реализация. Такъв модел се реализира от структурата на Фон Нойман на компютъра. За моделиране на процесите на реализиране на паралелно изпълнение на елементарни операции в теорията на алгоритмите се използва моделът на "екип от калкулатори". Всяка подзадача се решава от калкулатор, който, ако е необходимо да получи или предаде информация за други подзадачи, я обменя с други калкулатори. В същото време не е изключена възможността за решаване на един прост проблем, който не е свързан с други, с един калкулатор, например при изчисляване на ab + cde. Всички калкулатори работят едновременно във времето, изпълнявайки функциите си паралелно. Удобно средство за описване на паралелизма на взаимодействащи процеси са графични модели от специална форма, наречени мрежи на Петри.
Мрежата на Петри е двустранен граф (т.е. такъв граф, чието множество от върхове е разделено на две непресичащи се подмножества, така че всяко ребро на графа има един край в едно подмножество, а другият в друго подмножество) и съдържа върхове от два типа - позиции и преходи, а също така има насочени ръбове-дъги, които могат да свързват върхове от различни типове. На фиг.9.7. Даден е прост пример за мрежа на Петри, където кръговете представляват върховете, наречени позиции, а вертикалните линии, върховете, наречени преходи. Наборът от позиции, които са свързани с определен преход чрез дъги, насочени към него, се наричат входни позиции на този преход. Всички позиции, към които са насочени дъгите от прехода, формират набора от изходни позиции на този преход. Всеки връх на графа, съответстващ напозиции на мрежата на Петри, може да се присвои неотрицателен брой етикети, които на фигурата са обозначени с точки вътре в кръга. Първоначалното разпределение на етикетите съответства на началните условия на мрежата и се нарича първоначално етикетиране.
По този начин мрежата на Петри N може да бъде дефинирана чрез следната четворка: N=0>, тук A и T са крайни набори от позиции и преходи, съответно: A=1. ak>, Т=1. tl>. При това АТ=, АТ. Функцията F дефинира връзки между позиции и преходи, така че
F(a,t)=
F(t,a)=
M0 определя първоначалното етикетиране на мрежата и е k-мерен вектор от неотрицателни числа, чийто j-ти елемент означава броя на етикетите в позиция aj.
За мрежа на Петри Фиг.9.7 k=l=5, М0= и
F(a,t)=
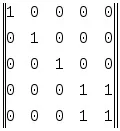
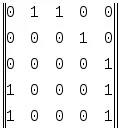
Ако всички позиции за въвеждане на преход ti съдържат етикети, тогава преходът е активен. Може да се реализира активен преход. Понякога активните преходи се наричат запалимост, а осъществяването на прехода се нарича неговото изгаряне. В резултат на изпълнението (изгарянето) на прехода се премахва по един етикет от всяка входна позиция и се поставя по един етикет на всяка изходна позиция. По този начин етикет на позиция може да се използва само за реализиране на един преход. Осъществяването на преход може да се разглежда като събитие, което се случва, когато са изпълнени определени условия, в резултат на което старите условия изчезват и се създават нови, докато общият брой на етикетите в мрежата може да се промени. Важно е, че не трябва да се изпълняват всички активни преходи, а могат да се изпълняват само активни преходи.
В мрежата на Петри на фиг. 9.7 началната маркировка, според която има маркировка в позиция a1, прави активен преход t1. След изпълнението на този преход, етикетът от a1 се премахва и етикетите се поставят вътрепозиции a2 и a3, което съответства на паралелизиране на процеса. След това се реализират преходи t2 и t3 и се появяват етикети при a4 и a5. Тези събития могат да се появят в различни моменти от време, тъй като се отнасят до различни паралелни процеси. Въпреки това, нито t4, нито t5 могат да бъдат приложени, докато и двата процеса не приключат. Тогава се реализира един от преходите t4 или t5 и мрежата на Петри преминава в начално състояние.
Мрежата на Петри е удобен и нагледен инструмент за описание на взаимодействащи процеси. Потокът на процеса съответства на последователността от преходи, което кара етикетите да се движат в мрежата, т.е. променящи се състояния на процеса.
Приложение 2 предоставя допълнителен материал за паралелни изчисления.