Алгоритъм за определяне дали дадена точка попада в контур въз основа на комплексен анализ
.collapse">Съдържание
Здравейте на всички хора на Habr. Искам да представя на уважаемите читатели пример, когато висшата математика, суха и далеч от живота в нашето разбиране, даде не лош практически резултат.

Първо малко спомени
Беше, когато бях студент в един от техническите университети през 90-те години, може би втора година. Някак си стигнах до олимпиадата по програмиране. И на тази олимпиада имаше задача: да се зададат координатите на триъгълник, тестова точка на равнината, и да се определи дали тази точка принадлежи към областта на триъгълника. Като цяло, дребен проблем, но тогава не го реших. Но тогава се замислих за по-обща задача - принадлежност към сметище. Повтарям - беше средата на 90-те, нямаше интернет, нямаше книги по компютърна геометрия, но имаше лекции за кулата и лаборатория 286 с турбо паскал. И така звездите съвпаднаха, че точно по времето, когато си мислех за проблема, те ни четоха теорията за комплексна променлива на кулата. И една формула (за нея по-долу) падна на плодородна почва. Алгоритъмът беше измислен и имплементиран в Pascal (за съжаление моят винт от един и половина гигабайта умря и отнесе този код и куп други мои младежки разработки в забрава). След института постъпих на работа в един изследователски институт. Там трябваше да се занимавам с разработването на ГИС за нуждите на служителите на института, като една от собствените ми задачи беше да определям дали обектите попадат в контура. Алгоритъмът беше пренаписан на C++ и се оказа отличен при работа.
Задача за алгоритъма
Определете:
дали точката принадлежи на областта D, ограничена от многоъгълника.
Извеждането на формули за последващо писане на алгоритъма по никакъв начин не претендира за товаматематическа пълнота и точност, но само демонстрира инженерния (потребителски подход) към кралицата на областите на науката.
Интегрална формула на Коши
Обяснение от работническо-селска инженерна гледна точка: - границата G е нашият зададен контур, - z0 -тествана точка - f (z) - комплексната функция на комплексния аргумент не отива до безкрайност никъде в контура.
Тоест, за да установим дали една точка принадлежи на контур, трябва да изчислим интеграла и да го сравним със стойността на функцията в дадена точка. Ако те съвпадат, тогава точката е в контура. Забележка: Интегралната теорема на Коши казва, че ако точката не лежи в контура, тогава интегралната функция не отива никъде в безкрайност, тогава интегралът е равен на нула. Това опростява въпроса - просто трябва да изчислите интеграла и да го проверите за равенство на нула: точката не е контурът, равен на нула, той е различен - лежи в контура. Нека изчислим интеграла. За f(z) вземаме проста функция 1. Без загуба на общност можем да вземем точка 0 за z0 (винаги можете да изместите координатите).
Отърваваме се от въображаемата единица в знаменателя на интегранта и разделяме интеграла на реални и въображаеми части:
Получихме два криволинейни интеграла от втори род. Изчислете първия
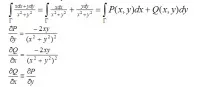
Условието интегралът да не зависи от пътя е изпълнено, следователно първият интеграл е равен на нула и не е необходимо да се изчислява.
С имагинерната част този трик не работи. Спомняме си, че нашата граница се състои от сегменти, получаваме: За да направите това, записваме уравнението на i-тия сегмент в параметричната форма
Заместете в интеграла
и след тромави и досадни трансформации получаваме следната измамна формула:
Накраяполучаваме
Алгоритъм в C++:
T – тип точка, например:structPointD double x,y; >;
Пример за това как работи алгоритъмът е написан с помощта на най-добрата 2D графична библиотека според мен: Геометрия против зърно (AGG).
Контроли: ляв бутон - добавяне на нова контурна точка десен бутон - затваряне на контура ляв бутон със задържан Shift - прехвърляне на тестова точка
Господа, които се интересуват, давам по-бърз алгоритъм. Вече не е моя. Специално и много благодаря на забравения за статията. template bool pt_in_polygon2(const T &test,const std::vector &polygon)
static const int q_patt[2][2]= < , >;