Алгоритми върху дървета
Съдържание
Диаметър на дървото[редактиране]
| Определение: |
| Диаметър на дърво(англ.diameter of a tree) — максималната дължина (в ръбове) на най-късия път в дървото между всеки два върха. |
Нека е дадена графиката [math]G = \langle V, E \rangle [/math]. Тогава диаметърът на [math]d[/math] е [math]\max\limits_ dist(v, u)[/math], където [math]dist[/math] е най-късото разстояние между върховете.
Алгоритъм[редактиране]
- Вземете произволен връх [math] v \in V [/math] и намерете разстоянията до всички други върхове. [math]d[i] = dist(v, i)[/math]
- Вземете връх [math] u \in V [/math] такъв, че [math]d[u] \geqslant d[t][/math] за всеки [math]t[/math] . Отново намерете разстоянието от [math]u[/math] до всички други върхове. Най-голямото разстояние е диаметърът на дървото.
Ще търсим разстоянието до останалите върхове с помощта на алгоритъма [math]BFS[/math].
Внедряване[редактиране]
Обосновка за коректност[редактиране]
Ще използваме свойството, че всяко дърво има повече от едно листо. Изключителен случай е дърво от един връх, но и в този случай алгоритъмът ще работи правилно.
| Теорема: |
След като стартираме алгоритъма, получаваме дървото [math]BFS[/math] .
| Теорема: |
Да предположим, че има ребро [math]u, v[/math] между съседни поддървета:
Помислете за първия връх, до който ще доведе нашият алгоритъм, нека това е връх [math]u[/math] , тогава в хода на разглеждане на всички съседни върхове [math]u[/math] ще добавим връх [math]v[/math] към списъка, като по този начин елиминираме възможността те да попаднат в различни поддървета.
Намалихме проблема до намирането на връх [math]w[/math], така че сумата от дълбочините на поддървото да е максимална.
Нека докажем, че едно от търсените поддървета съдържа най-дълбокия лист. Ако не, тогава като вземем разстоянието от [math]w[/math] до най-дълбокия лист, можем да подобрим отговора.
Така доказахме, че трябва да вземем върха [math]u[/math] с най-голяма дълбочина след първия [math]BFS[/math], очевидно е, че трябва да го сдвоим с върха [math]w[/math], така че [math]dist(u, w)[/math] да е максимум. Върхът на [math]w[/math] може да бъде намерен чрез стартиране на [math]BFS[/math] от [math]u[/math] .
Очаквано време за работа[редактиране]
Всички операции с изключение на [math]BFS[/math] - [math]O(1)[/math] . [math]BFS[/math] работи в линейно време, изпълняваме го два пъти. Получаваме [math]O(V + E)[/math] .
Център на дървото[редактиране]
Дефиниции [редактиране]
| Определение: |
| Ексцентричността на връх [math]e(v)[/math](англ.eccentricity of a vertex) е [math]\max\limits_dist(v, u)[/math] , където [math]V[/math] е множеството от върхове на свързания граф [math]G[/math] . |
| Определение: |
| Радиус[math]r(G)[/math](англ.radius) е най-малкият от ексцентрицитетите на върха на графиката [math]G[/math] . |
| Определение: |
| Централен връх(англ.central vertex) е връх на графиката [math]G[/math], така че [math]e(v) = r(G)[/math] |
| Определение: |
| Центърът на графиката [math]G[/math](англ.center of a graph) е множеството от всички централни върхове на графиката [math]G[/math] . |
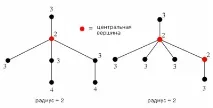
Алгоритъм[редактиране]
Наивен алгоритъм[редактиране]
Намерете центъра на графиката въз основа на нейната дефиниция.
- Конструирайте матрицата [math]A_[/math] ( [math]n[/math] е кардиналността на множеството [math]V[/math]), където [math]a_ = d_[/math] , тоест матрицата на най-кратките пътища. За да го създадете, можете да използвате алгоритъма на Floyd-Warshall или Dijkstra.
- Нека изчислим максимума във всеки ред на матрицата [math]A[/math] . Така получаваме масив с дължина [math]n[/math] .
- Нека намерим най-малкия елемент в този масив. Този връх е центърът на графиката. В случай, че има няколко върха, всички те са центрове.
Асимптотичното поведение зависи от метода, използван за изчисляване на най-кратките пътища. При Floyd това ще бъде [math]O(V^3)[/math] , а при Dijkstra това ще бъде максимумът от асимптотиката на конкретно изпълнение на Dijkstra и [math]O(V^2)[/math] , за които намираме максимумите в матрицата.
Дървовиден алгоритъм в O(n) [редактиране]
Всъщност алгоритъмът за намиране на центъра е описан в доказателството на теоремата.
- Нека преминем през дървото, като преминем в дълбочина и маркираме всички висящи върхове с числото [math]0[/math] .
- Отрежете маркираните върхове.
- Получените листа ще бъдат маркирани с числото [math]1[/math] и също ще бъдат отрязани.
- Ще повтаряме, докато няма повече от две листа на текущата дълбочина и в същото време също няма да има повече от две листа в дървото.
Останалите листа са в центъра на дървото.
За да работи алгоритъмът в [math]O(n)[/math], трябва да обработвате листата един по един, като поддържате два слоя, последователни в дълбочина в опашката.