Чебишев П
Чебишев П.Л.
През 1850 г. П. Л. Чебишев извежда формула, търсена напразно от най-видните математици, за определяне с голяма точност на броя на простите числа между 1 и всяко число х. Тъй като в момента има таблица с прости числа между 1 и 10 000 000, лесно е да се провери степента на точност на формулата на Чебишев в тези граници.
Означавайки, както е обичайно в математиката, реалния брой прости числа между 1 и числото x със символа π (x) (чете се, pi от x), а броят им, изчислен по формулата на Чебишев, със символа Li (x) (независимо дали от x), намираме разликата между тях, т.е. Li (x) - π (x) за различни стойности на x. Тези разлики показват колко резултатът, изчислен по формулата на Чебишев, се отклонява от истинската стойност на желания брой прости числа.
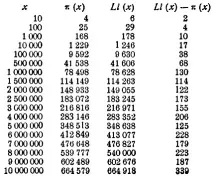
Таблицата показва, че числата, получени по формулата на Чебишев, в рамките на 10 000 000, винаги са малко по-големи от действителните числа на простите числа, но това отклонение е само около 0,16% за 500 000 и само 0,05% за 10 000 000. Точността на формулата на Чебишев е много висока и нараства с увеличаване на числото x.

Обърнете внимание, че следното неочаквано свойство на числата на Чебишев вече е доказано. В естествения ред, много далеч отвъд 10 000 000, има число, около което Li (x) влияе не повече, а по-малко от числото π (x). През 1933 г. е установено, че това е случаят с числото x, което се определя от приблизителното равенство
Числото на Eyu (така нареченото число на Skewes) е най-голямото число, срещано някога в науката. Това е числото, в което единицата е последвана от
ОТНОСНОЗа впечатлението, направено от откритието на Чебишев на формулата за определяне на броя на простите числа, може да се съди по мненията на водещи математици.
Известният английски математик Силвестър (1814-1897) нарече Чебишев „победител на простите числа, който пръв ограничи капризния им поток в алгебрични граници“ и добави, че „по-нататъшни успехи в теорията на простите числа могат да се очакват само когато се роди някой, който превъзхожда Чебишев в своята проницателност и замисленост толкова, колкото Чебишев надминава обикновените хора в тези качества“.

P. L. Chebyshev едновременно реши още един проблем, който беше останал нерешен преди.
Френският математик Бертран (1822-1900) проверява за всички числа до 6 000 000 наличието на следната закономерност: за всички числа х, започвайки от 4, между числата х и 2 х-2 има поне едно просто число. Това твърдение е известно като „предпоставки (постулат)“ на Бертран4. П. Л. Чебишев доказва предложението на Бертран и го превръща в теорема.

От всичко, което е казано за P. L. Chebyshev, може да се мисли, че той е теоретик, който се занимава с най-абстрактните области на математиката, далеч от всякаква практика.

Междувременно той е учен, който по-често от всеки друг математик е решавал проблеми, произтичащи от практическите нужди на човека.
Това може да се съди вече по заглавията на неговите произведения, сред които откриваме следните: "За един механизъм", "За зъбни колела", "За най-простите съединения", "За кроене на рокли" и др. Той изучава структурата на вятърни мелници, различни фабрични инсталации и, според него, навсякъде се натъква на въпроси на математиката, за коя науказнаеше малко за времето си.

П. Л. Чебишев запълни тези празнини в науката със своите гениални теоретични трудове.
Успоредно с това през целия си живот той се занимава с практическа механика, изобретява голям брой механизми, прави опити със стрелба и много допринася за постигането от българската артилерия на онова високо съвършенство, с което винаги се е славела артилерията на всички европейски държави.
Всички дейности на Чебишев представляват постоянна комбинация от теория и практика; Тази дейност се ръководи от същата идея, която според Чебишев е в основата на цялата човешка дейност: как да постигнете най-добри резултати с най-малко усилия, как да разполагате със средствата си, за да постигнете възможно най-голяма полза. Прилагайки тази идея за подобряване на средствата за изчисление, той дава формули, използването на които от един от неговите талантливи последователи, академик А. Н. Крилов, позволява да се подобрят изчисленията на корабостроенето до такава степен, че България в това отношение е по-висока от останалия свят в продължение на много десетилетия.
Накрая трябва да се отбележи, че П. Л. Чебишев създава първата българска математическа научна школа, чиято отличителна черта е решаването, по възможност с прости средства, на конкретни въпроси, довеждайки решението до формула, чрез която може да се получи числен резултат.
Към тази школа принадлежат почти всички известни имена на българските математици от втората половина на 19 и началото на 20 век: А. Н. Коркин, Е. И. Золотарев, А. М. Ляпунов, А. А. Марков, Г. Ф. Вороной, В. А. Стеклов, А. Н. Крилов и много други.