Дифракционна граница на разделителна способност на оптични инструменти, ТОВА Е ФИЗИКА
За практиката най-интересният случай е дифракцията на светлината, когато препятствието оставя отворена само малка част от 1-вата зона на Френел. Този случай се реализира при условие
т.е. дифракционната картина от малки препятствия трябва в този случай да се наблюдава на много големи разстояния. Например, ако R = 1 mm, λ = 550 nm (зелена светлина), тогава разстоянието L до равнината на наблюдение трябва да бъде значително по-голямо от 2 метра (т.е. минимум 10 метра или повече). Лъчите, проведени до далечна точка на наблюдение от различни елементи на вълновия фронт, практически могат да се считат за паралелни. Този случай на дифракция се нарича -дифракция в успоредни лъчи илидифракция на Фраунхофер - на името на немския физик Йозеф Фраунхофер, съвременник на Френел. Ако на пътя на лъчите зад препятствието се постави събирателна леща, тогава паралелен сноп от лъчи, дифрагиран върху препятствието под ъгъл θ, ще се събере в някаква точка от фокалната равнина (фиг. 3.9.1). Следователновсяка точка във фокалната равнина на лещата е еквивалентна на точка в безкрайност в отсъствието на леща.
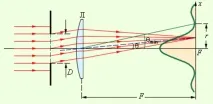
Дифракция в успоредни лъчи. Зелената крива е разпределението на интензитета във фокалната равнина (мащабът по оста x е значително увеличен)
Дифракционната картина на Фраунхофер се наблюдава във фокалната равнина на лещата. Но според геометричната оптика точково изображение на отдалечен точков обект трябва да бъде разположено във фокуса на лещата. Всъщност изображението на точков обект е замъглено поради дифракция. Това е вълновата природа на светлината.
Никоя оптична система не може да създаде точков образ. В случай на дифракция на Фраунхофер от кръгъл отвор с диаметър D, дифракциятаизображението се състои от централно светлинно петно (Airy disk), което представлява приблизително 85% от светлинната енергия, и светли и тъмни пръстени около него (фиг. 3.9.2). Това дифракционно петно се приема като изображение на точков източник. Радиусът на централното петно във фокалната равнина на лещата е
Ако лъчите на светлината от далечен източник падат директно върху лещата, тогава ролята на екрана, върху който се дифрактира светлината, се изпълнява от рамката на лещата. В този случай D трябва да се разбира като диаметър на лещата.

Дифракционно изображение на точков източник (дифракция от кръгъл отвор). Приблизително 85% от светлинната енергия навлиза в централното петно
Размерът на дифракционните изображения е много малък. Например, радиусът на централното светло петно във фокалната равнина на леща с диаметър D = 5 cm и фокусно разстояние F = 50 cm в монохроматична светлина с дължина на вълната λ = 500 nm е приблизително равен на 0,006 mm. При много оптични устройства (камери, проектори и др.) дифракционното замъгляване на изображенията се маскира от много по-силни изкривявания поради несъвършенството на оптиката. Но във високопрецизните астрономически инструментиограничението за качество на дифракцията на изображенията е реализирано. Поради дифракционното замъгляване изображенията на две близки точки на обект може да не се различават от изображението на една точка. Да разгледаме като пример лещата на астрономически телескоп, насочен към две близки звезди, разположени на ъглово разстояние ψ една от друга. Предполага се, че всички дефекти и аберации са елиминирани и във фокалната равнина на лещата се наблюдават дифракционни изображения на звезди (фиг. 3.9.3).
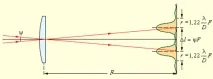
Дифракционни изображения на две близки звезди във фокалната равнина на обектив на телескоп
На фиг. 3.9.3 разстояние Δl междуцентрове на дифракционни изображения на звезди надвишава радиуса r на централното светло петно - в този случай изображенията на звездите се възприемат от наблюдателя отделно и следователно лещата на телескопа позволява да се разделят две близки звезди. Тъй като ъгловото разстояние ψ между звездите намалява, дифракционните изображения могат силно да се припокриват и вече да не се различават от изображението на една звезда. В този случай обективът на телескопа не разпознава близките звезди. Английският физик Дж. Рейли в края на 19 век. предложено условно да се счита разделителната способност за пълна, когато разстоянието Δl между центровете на изображенията е равно (или надвишава) радиуса r на диска на Airy (фиг. 3.9.4).Условието Δl = r се наричакритерий за разделителна способност на Rayleigh. От този критерий следва:
Телескоп с диаметър на лещата D = 1 m може да раздели две звезди, разположени на ъглово разстояние ψmin = 6,7·10 –7 rad (за λ = 550 nm).
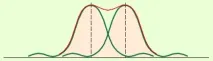
Ограничение на разделителната способност на Релей. Червената крива е разпределението на общия интензитет на светлината
Космическият телескоп Хъбъл, изведен в орбита през 1990 г., има огледало с диаметър D = 2,40 м. Максималната ъглова разделителна способност на този телескоп при дължина на вълната λ = 550 nm е: ψmin = 2,8 10 -7 rad. Работата на космическия телескоп не се влияе от атмосферните смущения. За да характеризирате лещата на телескопа, можете да въведете стойността R, реципрочната на ограничаващия ъгъл ψmin. Тази стойност се наричаразрешаваща способност на телескопа :
За да увеличите разделителната способност на телескопа, трябва да увеличите диаметъра на обектива (или да преминете към по-къси дължини на вълните). Всичко казано по-горе за разделителната способност на телескопа е приложимо за невъоръжено око. Окото, когато гледа отдалечени обекти, действа по същия начин като лещата на телескопа. Ролята на D играе диаметъра на зеницата на окото dsp.Ако приемем dsp = 3 mm, λ = 550 nm, намираме за граничната ъглова разделителна способност на окото
Този резултат е в добро съответствие с физиологичната оценка на разделителната способност на окото, базирана на размера на светлочувствителните елементи на ретината (пръчици и колбички).
Сега може да се направи едно общо заключение: светлинен лъч с диаметър D и дължина на вълната λ изпитва дифракционно разширяване поради вълновата природа на светлината.Ъгловата полуширочина φ на лъча се оказва от порядъка на λ / D, така че общата ширина d на лъча на разстояние L е приблизително равна на
Ориз. 3.9.5 качествено показва как светлинният лъч се трансформира, докато се отдалечава от препятствието.
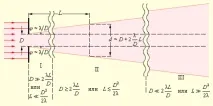
Светлинен лъч, който се разширява поради дифракция. Регион I - понятието светлинен лъч, законите на геометричната оптика. Регион II - зони на Френел, петно на Поасон. Област III - дифракция в успоредни лъчи
Оценките, направени на фиг. 3.9.5 показват, че ъгловата дивергенция на лъча намалява с увеличаване на първоначалния му напречен размер D. Това заключение е валидно за вълни от всякаква физическа природа. За да изпратите например "тесен" лъч лазерно лъчение към Луната, първо трябва да го разширите. Това се постига с телескоп: лазерният лъч се насочва в окуляра и след като премине през телескопа, излиза от обектива с диаметър D (фиг. 3.9.6).
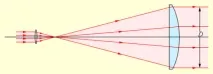
Разширяване на лазерния лъч с помощта на телескопична система
Такъв разширен лъч, достигайки до Луната, ще „освети“ петно от нейната повърхност с радиус , където L е разстоянието до Луната. Като вземем D = 2,5 m (рефлекторен телескоп на Кримската обсерватория), λ = 550 nm, L = 4 10 6 m, получаваме R ≈ 90 m.чийто радиус би бил 250 пъти по-голям.
Разделителна способност на микроскопа. С помощта на микроскоп се наблюдават близко разположени обекти, поради което неговата разделителна способност се характеризира не с ъгловото, а с линейното разстояние между две близки точки, които все още могат да се възприемат отделно. Наблюдаваният обект се намира близо до предния фокус на обектива. Често пространството пред обектива се запълва със специална прозрачна течност -имерсия (фиг. 3.9.7). В равнината, геометрично свързана с обекта, се намира неговият увеличен образ, който се гледа от окото през окуляра. Изображението на всяка точка е замъглено поради дифракция на светлината.
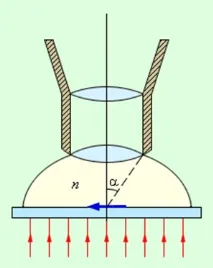
Имерсионна течност пред обектива на микроскопа
За първи път границата на разделителна способност на микроскопска леща е определена през 1874 г. от немския физик Херман Хелмхолц.Формулата на Хелмхолц има формата:
Тук λ е дължината на вълната, n е индексът на пречупване на потапящата течност, α е така наречениятъгъл на отвора (фиг. 3.9.7). Стойността n sin α се наричачислова апертура.
За добрите микроскопи ъгълът на отвора α е близо до неговата граница: α ≈ π / 2. Както може да се види от формулата на Хелмхолц, използването на потапяне донякъде подобрява границата на разделителната способност. Приемайки за оценки sin α ≈ 1, n ≈ 1,5, получаваме:
По този начин, използвайки микроскоп, е фундаментално невъзможно да се изследват детайли, които са много по-малки от дължината на вълната на светлината. Вълновите свойства на светлината определят границата на качеството на изображението на обект, получено с помощта на всяка оптична система.