Дисперсионен анализ
Дисперсионният анализ (от латинското Dispersio - дисперсия / на английски Analysis Of Variance - ANOVA) се използва за изследване на влиянието на една или повече качествени променливи (фактори) върху една зависима количествена променлива.
Еднопосочен дисперсионен анализ
Еднопосочният дисперсионен анализ се използва за тестване на хипотезата, че математическите очаквания на няколко популации са еднакви. Например, ако искате да разберете дали входът x влияе върху изходната зависима променлива y. В този пример входната променлива x приема дискретни стойности, а изходната променлива y е непрекъсната случайна променлива, чийто вероятностен характер се дължи на наличието на допълнителен шум e.
Еднопосочният анализ на дисперсията се основава на следните предположения:
При всяко наблюдениеeiима нормално разпределение с нулева средна стойност и крайна дисперсия.
За всякаiдисперсияeiе постоянна стойност.
Нека разгледаме изчислителната процедура за еднопосочен дисперсионен анализ. Некаxприемаkразлични стойности или, както се казва, факторътxимаkнива. Нека всяко ниво имаnнаблюдения на изходната стойностy. Тогава резултатите могат да бъдат представени под формата на таблица (колони - нива на факторx, редове - наблюденияy):
| номер на наблюдение | Нива на входния факторx | ||||
| 1 | 2 | … | й | … | |
| 1 | y 11 | y 12 | … | y 1j | … |
| 2 | y 21 | y 22 | … | y 2j | … |
| … | … | … | … | … | … |
| аз | y i1 | y i2 | … | yij | … |
| … | … | … | … | … | … |
| н | y n1 | y n2 | … | y nj | … |
Ако нивата на фактора x не влияят на математическото очакване y, тогава всички наблюдения са извадка от една и съща обща съвкупност (при условие, че горните условия са изпълнени). Тогава дисперсията на генералната съвкупност може да бъде оценена чрез две независими оценки: чрез средните стойности на y за всяко от нивата x или като средна аритметична стойност на оценките на дисперсиите y за всяко от нивата x. Първата оценка се нарича оценка на дисперсията на нивотоS2 Lv, втората се нарича оценка на дисперсията на грешкатаS2 Err.
y.j. Средно за j-то ниво;
Ако няма влияние на нивата на фактора x върху математическото очакване, тогава отношениетоF=S2 Lv/S2 Err се подчинява на закона за разпределение на Фишер. Характеристиките на това разпределение зависят от броя на степените на свобода на оценкитеs2 LV иS2 грешка (броят на степените на свобода на числителяν1 = (k-1)и деноментораν2 2). За всяко дадено ниво на значимостαвинаги има критична стойност F crit, която F може да превиши при отсъствие на влиянието на ниваxс вероятност не повече отα. Това означава, че ако в резултат на обработката на данни изчислената стойност на F-статистиката надвишава съответния F crit, тогава данните противоречат на хипотезата, че математическите очаквания y са равни за всички нива x. АкоFF крит, тогава данните не противоречат на тази хипотеза и трябва да се приеме, че x нивата не влияят на математическитечака y.
Двупосочен дисперсионен анализ
При двуфакторния дисперсионен анализ хипотезата за равенството на математическите очаквания на изходния контролиран параметърyсе тества на различни нива на два фактора.
В този модел входните променливиx 1иx2приемат дискретни стойности, а изходната променлива y е непрекъсната случайна променлива, чийто вероятностен характер се дължи на наличието на допълнителен шум e.
Двупосочният анализ на дисперсията се основава на следните допускания:
При всяко наблюдениеeiима нормално разпределение с нулева средна стойност и крайна дисперсия.
За всякаiдисперсияeiе постоянна стойност.
Разгледайте изчислителната процедура за двуфакторен дисперсионен анализ. Некаx 1приема k различни стойности, или факторътx 1има k нива,x2приема m различни стойности, или факторътx2има m нива. Нека всяка от комбинациите от нива имаnнаблюдения на изходната стойностy. След това резултатите могат да бъдат представени под формата на таблица:
| Нива на входния факторx2 | Нива на входния фактор x1 | ||||
| 1 | 2 | … | й | … | |
| 1 | y111 … y11n | y121 … y12n | … | y1j1 … y1jn | … |
| 2 | y211 … y21n | y221 … y22n | … | y2j1 … y2jn | … |
| … | … | … | … | … | … |
| аз | yi11 … yi1n | yi21 … yi2n | … | yij1 … yijn | … |
| … | … | … | … | … | … |
| м | ym11 … ym1n | ym21 … ym2n | … | ymj1 … ymjn | … |
Ако нивата на факторитеx 1иx 2не влияят на очакванетоy, тогава всички наблюдения са извадка от една и съща генерална съвкупност (при условие, че горните условия са изпълнени). След това дисперсията на генералната съвкупност може да бъде оценена чрез следните независими оценки: чрез средните стойностиyза всяко от нивата на факторитеx 1илиx 2или като средно аритметично от оценките на дисперсиитеyза всяко от ниватаx 1или <1 2>x 2. Както при еднопосочния ANOVA, първата оценка се нарича оценка на дисперсията на нивотоS2 Lv, втората се нарича оценка на дисперсията на грешкатаS2 Err.
За първия и втория фактор имаме:
y .j.. Средно за j-то ниво на първия фактор;
y i... Средно заi-то ниво на втория фактор;
y . . Обща авария.
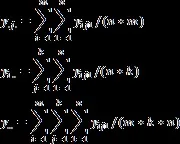
Оценката на дисперсията на грешката се изчислява по формулата:
y ij.. Средна стойностyна j-то ниво на първия фактор иi-то ниво на втория фактор.
Наличието на два фактора позволява използването на друга оценка на дисперсията - взаимодействието:
Ако нивата на факторитеx1 иx2 не влияят на математическото очакване, тогава съотношениятаF1=S2Lv1/S2 Err,F2=S2Lv2/S 2ErrиF In t=S2 Int/S 2 Err се подчиняват на закона за разпределение на Фишер. Характеристиките на това разпределение зависят от броя на степените на свобода на оценкитеS2Lv1,S2Lv2,S2 Int иS2 Err (броят степени на свобода на числителяν1=(k-1),ν2=(m-1),νInt=(m-1)*(k-1) и знаменателνErr=m*k*(n-1) ). За всяко дадено ниво на значимостαвинаги има критична стойностF crit, коятоFможе да надхвърли при липса на влияние на нивата на факторитеx1,x2 и тяхното взаимодействиеx1*x2 с вероятност не повече отα. Това означава, че ако в резултат на обработката на данните изчислената стойност на F-статистиката надвишава съответнатаF crit, тогава данните противоречат на хипотезата за равенството на математическите очаквания y за всички нива на факторитеx1,x2 и тяхното взаимодействиеx1*x2. АкоFF crit, тогава данните не противоречат на тази хипотеза и трябва да се приеме, че нивата не влияят на очакваниятаy.