Добавяне и изваждане на десетични числа, платформа за съдържание

Събиране и изваждане на десетични знаци
Правилото за запаметяване в учебника е формулирано по следния начин:
За да добавите (извадите) десетични дроби, трябва: 1) да изравните броя на десетичните знаци в тези дроби; 2) да ги напишете една под друга, така че запетаята да е написана под запетаята; 3) да извършите събиране (изваждане), като игнорирате запетаята; 4) да поставите запетаята под запетаята в тези дроби във вашия отговор.
Изображение:запетая е капка, която тече от лейка
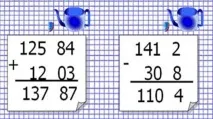
Ако първата изпусната или заменена с нула цифра е 5, 6, 7, 8 или 9, тогава цифрата пред нея се увеличава с 1. Ако първата изхвърлена или заменена с нула цифра е 0, 1, 2, 3 или 4, тогава цифрата пред нея остава непроменена.
Изображение:Числата 0, 1, 2, 3, 4 се наричат „малки“, а 5, 6, 7, 8, 9 се наричат „големи“. Отделяме цифрата, до която трябва да се закръгли числото. Само „големи“ числа могат да преминават през оградата, докато броят пред оградата се увеличава с единица

Умножение на десетични знаци
За да умножите две десетични дроби, трябва: 1) да извършите умножението, без да обръщате внимание на запетаите; 2) да отделите със запетая толкова цифри отдясно, колкото има след десетичната запетая в двата множителя заедно.
Изображение:в примерите за умножение на десетични дроби числата след десетичната запетая са маркирани с различен цвят, тъй като е необходимо да се преброи техният брой.

Десетично деление
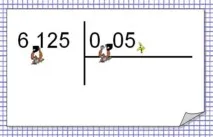
За да разделите число на десетична дроб, трябва да: 1) в делителя и делителя, преместете запетаята надясно толкова цифри, колкото има след десетичната запетая в делителя; 2) след това изпълнетеделение на естествено число.
Изображение:запетаите са две маймуни. Втората маймуна (в разделителя) има цел - да вземе банана, който се намира зад последната цифра. Тя се опитва да вземе банан, на свой ред първата маймуна (в дивидента) повтаря действията на втората маймуна, т.е. прескача толкова числа, колкото е прескочила втората.
Мерни единици за дължина, площ, обем
Изображение:когато преобразуваме едни мерни единици (дължина, площ, обем) в други, рисуваме стрелки, по които се движи малкото човече. Движейки се по стрелката, той събира нули, а движейки се срещу стрелката, дава нули.

Събиране и изваждане на дроби с различни знаменатели
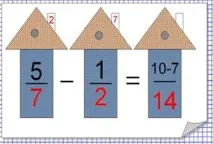
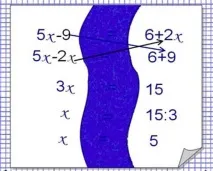
За да приведете дроби към общ знаменател, трябва: 1) да намерите най-малкото общо кратно на знаменателите на тези дроби, то ще бъде техният най-малък общ знаменател; 2) разделете най-малкия общ знаменател на знаменателите на тези дроби, т.е. намерете допълнителен фактор за всяка дроб; 3) умножете числителя и знаменателя на всяка дроб по нейния допълнителен множител.
Изображение:рисуване на къщи, като се обръща внимание на допълнителните мултипликатори, които се намират на покрива.

Модулът на числото не може да бъде отрицателен. За положително число и нула е равно на самото число, а за отрицателно число е равно на противоположното число.
Изображение:модулът е вана, а знакът минус е мръсотия. Намирайки се под знака на модула, отрицателното число се "измива" и излиза без знака минус - чисто. Във ваната както положителните, така и отрицателните числа могат да се „мият“ (тоест да стоят под знака на модула).

Събиране на числа с помощта на координатна линия
Изображение:специална роля играят "човечетата" ("положителни" и„Отрицателно“), което ви позволява визуално да симулирате „Математическо събиране на положителни и отрицателни числа“ в 6. клас.
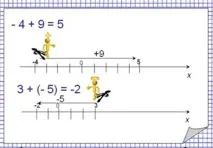
Събиране и изваждане на числа с различни знаци
За да съберете две числа с различни знаци, трябва: 1) да извадите по-малкото от по-големия модул от членове; 2) да поставите знака на члена, чийто модул е по-голям пред полученото число.
За да съберете две отрицателни числа, трябва: 1) да съберете техните модули; 2) да поставите знак „-” пред полученото число.
Изображение:Черните пулове са отрицателни числа, белите пулове са положителни числа. Правила на играта: пул от един цвят "изяжда" пул от друг цвят. Този с най-много пулове от кой цвят е победител.
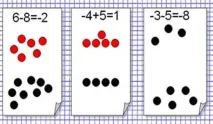
Корените на уравнението не се променят, ако някой член се прехвърли от една част на уравнението в друга, като същевременно се промени знакът му.
Изображение:знакът „=“ е река, а знакът на термина „+“ или „-“ е облекло. Терминът преплува реката и сменя мокри (например плюс) дрехи със сухи (минус).
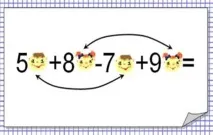
За да добавите (или да кажете: донесете) подобни термини, трябва да съберете техните коефициенти и да умножите резултата по общата буквена част.
Изображение:нарисувайте лица. Момичетата се "добавят" с момичета, момчета - с момчета.
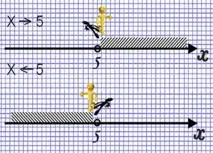
Изображение:Когато започнем да изучаваме неравенства, на учениците им е трудно да оцветят необходимата част от гредата. За да стане по-ясно за момчетата коя част от гредата да се излюпи, рисуваме знака за неравенство към стрелката. Стрелката показва посоката на люка.
Съотношения между страни и ъгли на правоъгълен триъгълник
Синусът на остър ъгъл в правоъгълен триъгълник е съотношението на срещуположния катет къмхипотенуза. Косинусът на остър ъгъл в правоъгълен триъгълник е отношението на съседния катет към хипотенузата.
Изображение:в синус, буквата "и" се променя на буквата "о", косинус, буквата "о" се променя на буквата "и".
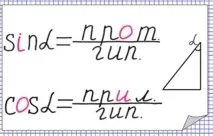
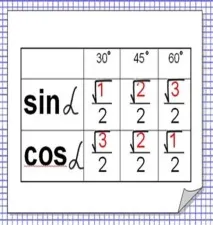
Стойности на основните ъгли на тригонометричните функции
Изображение:за да запомните стойностите на синуса и косинуса за ъгли от 30, 45 и 60 градуса, запомнете числата: за синуса 1, 2, 3, а за косинуса - 3, 2, 1, навсякъде в знаменателя 2, а в числителя знака на корена, но тъй като = 1, тогава не пишем знака на корена за 1.
Функция. Обхватът и обхватът на функцията. Свойства на функцията.
Функция е такава зависимост на променливата Y от X., при която всяка стойност на променливата X. съответства на една стойност на променливата Y. Всички стойности на независимата променлива формират домейна на дефиниция. Всички стойности, които независимата променлива приема, формират домейна на функцията. Изображение: X - родители, Y - деца; децата зависят от родителите си; всички родители формират област на значение, децата - област на дефиниция.
Функция се нарича нарастваща в определен интервал, ако по-голямата стойност на аргумента от този интервал съответства на по-голямата стойност на функцията; функция се нарича намаляваща в някакъв интервал, ако на по-голяма стойност на аргумента от този интервал съответства по-малка стойност на функцията.
Изображение:Нарастваща функция - вървим нагоре, намаляваща функция - слизаме по планината.
Дефиниране на аритметични и геометрични прогресии
Аритметичната прогресия е последователност, в която всеки член, започвайки от втория, е равен на предишния член, добавен към същото число.
ГеометриченПрогресията е поредица от ненулеви числа, всеки член от който, започвайки от втория, е равен на предишния член, умножен по същото число.
Изображение:разлика в аритметичната прогресия – стъпка, дължината на стъпката е постоянна; знаменателят на геометрична прогресия е скокът, дължината на скока се увеличава или намалява.

Функцията от дясната страна на равенството се приема със същия знак като оригиналната функция, ако приемем, че ъгълът n е ъгълът на първата четвърт.
За ъгли n±n и 2±n името на оригиналната функция се запазва; за ъгли n/2±n и 3/2n±n името на оригиналната функция се променя (синус към косинус, косинус към синус, тангенс към котангенс, котангенс към тангенс).
Изображение:формули за намаляване - правило на коня. Гледайки единична окръжност, а именно p / 2 и 3p / 2 (разположени на ординатната ос) - кимаме с глава отгоре надолу, когато гледаме p и 2p (разположени на абсцисната ос) - поклащаме глава отляво надясно.