Движение на материална точка
Да имате представа за свободни и несвободни материални точки, за силите на инерцията, за използването на силата на инерцията за решаване на технически проблеми.
Да познава формулите за изчисляване на силата на инерцията при транслационни и въртеливи движения, да познава принципа на д'Аламбер и да може да определя параметрите на движение, използвайки законите на динамиката и метода на кинетостатиката.
Безплатни и небезплатни точки
Материална точка, чието движение в пространството не е ограничено от никакви връзки, се наричасвободна.Задачите се решават с помощта на основния закон на динамиката.
Материалните точки, чието движение е ограничено от връзки, се наричат несвободни.
За несвободните точки е необходимо да се определят реакциите на връзките. Тези точки се движат под действието на активни сили и реакциите на връзки (пасивни сили), които ограничават движението.
Несвободните материални точки се освобождават от връзки: връзките се заменят с техните реакции. Освен това, небезплатните точки могат да се считат за безплатни (принцип на освобождаване от облигации).
Инерционна сила
Инертност— способността да се поддържа непроменено състояние, това е вътрешно свойство на всички материални тела.
Инерционната силае силата, която възниква при ускоряване или забавяне на тялото (материална точка) и е насочена в посока, обратна на ускорението. Силата на инерцията може да се измери, тя се прилага към "връзки" - тела, свързани с ускоряващо или забавящо тяло.
Изчислено е, че силата на инерцията е равна на
 |
Ускоряващото тяло (платформа с масаt)не възприема силата на инерцията, в противен случай ускорението на платформата изобщо би било невъзможно.
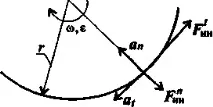
С въртеливо движение (криволинеен)полученото ускорение обикновено се представя като два компонента: нормалноanи тангенциалнопри.
Следователно, когато се разглежда криволинейно движение, могат да възникнат два компонента на инерционната сила: нормална и тангенциалнаa=at + an;
При равномерно движение по дъга винаги възниква нормално ускорение, тангенциалното ускорение е нула, следователно действа само нормалната компонента на инерционната сила, насочена по радиуса от центъра на дъгата.
Кинетостатичен принцип (принцип на Д'Аламбер)
Принципът на кинетостатиката се използва за опростяване на решаването на редица технически проблеми.
В действителност силите на инерцията се прилагат към телата, свързани с ускоряващото тяло (към връзките).
d'Alembert предложиусловно да се приложисилата на инерцията към активно ускоряващо се тяло. Тогава системата от сили, приложени към материалната точка, става балансирана и е възможно да се използват уравненията на статиката при решаване на задачи на динамиката.
Материална точка под действието на активни сили, реакции на връзки и условно приложена инерционна сила е в равновесие: