Електронно въртене
В предишната статия показахме, че всяка посока на въртене в квантовата механика съответства на един или друг вектор на състоянието. Откъде идват числените стойности на векторите на състоянието за посоките на определени оси? Оказва се, че
всяка измерима величина в квантовата механика съответства на матрица,
включително гърба. Освен това,
след измерването системата се описва от един от собствените вектори на матрицата на измерената стойност.
Какво е собствен вектор е най-лесно да се разбере на примера на обикновените вектори. Матрицата в този случай изразява някакво действие с вектори (въртене, мащабиране, изместване и т.н.). Умножавайки матрица по вектор, получаваме друг вектор (завъртян, увеличен по размер). Например, следната матрица се мащабира (увеличава с коефициент 2) в посока на диагонала x=y.
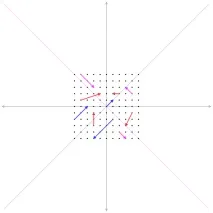
Собствените вектори на матрицата са тези, които не променят посоката си, когато са изложени на дадена матрица. Сините и розовите в анимацията са собствените вектори на дадената трансформация (матрица). Собствените вектори са съчетани със собствени стойности. Собствената стойност е просто число, показващо колко пъти дължината на собствения вектор се е променила по време на трансформацията. В розовото в нашия случай собствената стойност е равна на едно (дължината не се е променила), а в синьото е 2 (удвоила се е). Математически всичко по-горе може да се формулира по следния начин: ако векторът \(\displaystyle \boldsymbol \) е собствен вектор на матрицата M, тогава умножаването на матрицата по този вектор се свежда до умножаване по числото \(\displaystyle \lambda \) (собствената стойност):
\(\displaystyle \hat\boldsymbol=\lambda \boldsymbol \), ако \(\displaystyle \boldsymbol \) е собствен вектор
И така, спиновата матрицаОста z на Pauli изглежда така:
Неговите собствени вектори са векторът на състоянието на електрона със въртене нагоре (собствена стойност +1):
и надолу (собствена стойност -1):
Проверете дали при умножаване на матрицата по тези вектори, получаваме същите, умножени по собствената стойност. Собствените стойности играят специална роля в квантовата механика.
Собствените стойности са онези стойности, които могат да бъдат получени чрез измерване на стойността, описана от тази матрица.
В случай на спинови матрици, това е +1 или -1, съответстващо на измереното въртене "нагоре" и "надолу". Това е математическо описание на ефекта на квантуване: ние не можем да получим въртенето по друг начин, когато измерваме, тъй като тази матрица няма други собствени стойности. Същата причина например се крие в дискретността на енергийните нива в атомите: енергията е измерима величина и съответно също се описва с матрица.
Другите две спинови матрици по отношение на осите y и x са:
Техните собствени стойности също са +1 и -1 и ние вече сме дали собствените вектори.
Забелязвате ли симетрията на матриците? Това не е случайно. Измерените величини отговарят само на ермитови матрици. Техните собствени стойности и диагонални елементи са реални числа, а останалите елементи са симетрични по отношение на диагонала и са комплексно спрегнати един на друг.
Сега дори можем да изчислим вероятността да измерим една или друга стойност на въртенето на електрона спрямо всяка ос, а не само взаимно перпендикулярни x, y и z. Точно както обикновен вектор \( \displaystyle v\) може да бъде разложен на три базови вектора със съответните координати \( \displaystyle v_,v_,v_\), матрицата за измерване на въртене около всяка ос може да бъде съставена от матрици на Паули:
\(\displaystyle \hat\cdot\boldsymbol=v_\begin 0 & 1\\ 1 &0 \end+v_\begin 0 & -i\\ i &0 \end+v_\begin 1 & 0\\ 0 &-1 \end\) където \(\displaystyle v_, v_,v_\) са координатите на правилен вектор \(\displaystyle v\), указващ посоката на оста (само числа). Нека, например, намерим вероятността електрон със въртене "нагоре" около оста y да се върти "нагоре" около 45° завъртяна ос в равнината x-y. Електрон със въртене "нагоре" около оста y се описва от собствен вектор на матрицата \(\displaystyle \hat> \) със собствена стойност +1. Повдигали сме го и преди:
\(\displaystyle \rightarrow\rangle = \frac>\binom\)
Вектор, завъртян на 45°, е например (нормален) вектор с координати \(\displaystyle (1, 1, 0)\) или \(\displaystyle (1/\sqrt, 1/\sqrt, 0)\), ако дължината му е намалена до единица. Матрицата, съответстваща на измерването на въртенето около тази ос, е:
Неговият собствен вектор със собствена стойност +1 е:
За да се намери вероятността, е необходимо да се повдигне на квадрат абсолютната стойност на амплитудата на вероятността:
\(p=\langle\nearrow\rightarrow\rangle ^\приблизително 0,8536\)
Интуитивно може да се приеме, че ако при ъгъл 0° 100% от електроните са отклонени, а при ъгъл 90° 50% са отклонени, тогава при ъгъл 45° трябва да се отклонят 75% = 100-50/2. Интуицията предпочита линейно приближение. Точен резултат: 85,36%. И съвпада с аналитичния израз:
\(\displaystyle p=\frac\приблизително 0,8536\) с \(\displaystyle \alpha=\frac\)
Виждате ли, от някъде в матриците внезапно се появи косинусът. Така че класическата механика следва от квантовата механика.
В квантовата механика понятието оператор също се използва широко.Операторът е абстрактматематически обект, който в конкретен числов израз може да бъде представен с матрица (включително безкрайномерна). Подобно на вектор, който може да бъде написан по различен начин като координати в зависимост от основата или координатната система, един и същ оператор може да бъде изразен чрез различни матрици. Операторите често се обозначават с капачка в горната част, както направихме по-горе за спин операторите \(\displaystyle \hat\) (сигма. Гръцкиs. spin.). И понякога те изобщо не различават нищо - операторите в квантовата механика се използват по-често от обикновените променливи, така че по подразбиране всяка буква е оператор.
стойностите, чиито оператори не пътуват до работното място, не могат да бъдат измерени едновременно.
Невъзможно е едновременно измерване на въртенето около две оси. В случая на операторите за позиция и импулс този факт е по-известен като принципа на неопределеността на Хайзенберг.
Според мен има грешка в намерения собствен вектор, който е завъртян на 45 градуса
Собствените вектори не са уникални. Моят вектор също е собствен. Проверете))