Елиптични PDE
Лаборатория #2
Тема: Числено решение на диференциал
Частични диференциални уравнения.
Целта на работата: Да се изследват изчислителните възможности на пакетаMathCADза решаване на някои уравнения на математическата физика с помощта на метода на мрежата.
Частичните диференциални уравнения изискват намиране на функция не на една, както при ODE, а на няколко променливи. Тези уравнения включват производни по отношение на различни променливи (частични производни). Частичните диференциални уравнения описват голямо разнообразие от физични явления и с тяхна помощ е възможно успешно да се моделират най-сложните явления и процеси (дифузия, хидродинамика, квантова механика, екология и др.). MathCAD има ограничени възможности по отношение на частични диференциални уравнения. С вградените функции могат да бъдат разрешени само някои от специалните случаи. С двете вградени функции multigrid и relax могат да бъдат решени само най-простите случаи на уравнението на Поасон.
Елиптични частични диференциални уравнения
Изследването на такова уравнение води до разглеждане на проблеми за електрически и магнитни полета, за стационарно топлинно състояние, проблеми на хидродинамиката, дифузия и др. Нека разгледаме решениятауравнението на Поасони неговата хомогенна форма -уравнението на Лаплас.
Ще търсим решението на уравнението на Поасон в някаква ограничена област
| (1) | (1) |
| (2) |
къдетоf, f1, f2, f3, f4 са дадени функции (задачата, състояща се в решаване на елиптично уравнение за дадени стойности на желаната функция на границата на изчислителната област, се наричапроблем на Дирихле.).
Да строим в районаравномерна правоъгълна мрежа със стъпкиhиlсъответно поxиy:
Желаната функция, използваща метода на мрежата (метод на крайната разлика), ще бъде представена чрез набор от нейните приблизителни стойности в възлите на мрежата.Нека заменим производните с отношения на крайна разлика:
, докато DE (1) ще бъде заменено от уравнение с крайни разлики (3).
Ние апроксимираме диференциалната задача (1) - (2) върху шаблона „кръст“ (Фиг. 1), в резултат на което получавамеимплицитна трислойна диференциална схема(3):
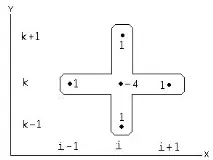
(3)
Където
За решаване на уравнението на Поасон в Mathcad се използва функциятаrelax
| отпуснете се(a, b, c, d, e, f, u, rjac) | Връща квадратната матрица на решението на уравнението на Поасон. Тукa, b, c, d, eса квадратни матрици с еднакъв размер, съдържащи коефициентите на уравнение (3); f е квадратна матрица, съдържаща стойностите на дясната страна на уравнение (3) във всяка точка от областта W, в която се търси решението; u е квадратна матрица, съдържаща граничните стойности на решението на границата на региона и първоначалното приближение за решението вътре в региона; rjac е число между 0 и 1, което контролира конвергенцията на алгоритъма. |
Заf= 0 получаваме уравнението на Лаплас:
| (4) |
Ако за уравнението на Лаплас в областта въведем решетка с еднаква стъпка по оситеxиy, тогава диференциалната схема (3) е значително опростена
(5)
Решението на уравнението на Лаплас с помощта на функциятаrelaxе показано по-долу.
Тестов случай.
Необходимо е да се намери разпределението на температурата вквадратна плоча, за която са определени гранични условия:
Разпределението на температурата се описва с уравнението на Лаплас:
Решение.
1. Нека въведем равномерна мрежа върху плочата с разстояние между възлите h.
Мрежата съдържа 25 възела, в 16 от които температурата е известна според граничните условия
3. Първоначалното приближение на температурните стойности в останалите 9 възела е вътре в мрежата - поставяме 0. Така,

Ще намерим стационарното разпределение на температурата в плочата с помощта на диференциалната схема (5) с помощта на вградената функция relax. (виж решение точка 4). Схема (5) дава система от 9 линейни алгебрични уравнения с девет неизвестни стойностиTвъв вътрешните възли на мрежата:
Като се вземат предвид граничните условия:


Забележка.Температурното разпределениеТима симетрия, съответстваща на симетрията на посочените в примера гранични условия.
5. Използвайки командата Graphics Create Contour Plot, показваме намереното разпределение на температурата в плочата на Фиг. 2
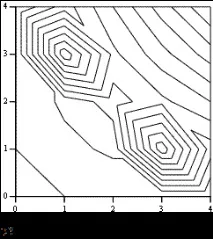 |
Задача.Намерете стационарното разпределение на температурата в квадратна плоча със страна 1, описана от уравнението на Лаплас
с гранични условия на формата
Решете проблема с помощта на функциятаrelax.
За да решите проблема, изградете решетка от 11 възела по протежение наx(i= 0, 1, .10) и 11 възела по протежение наy(j= 0, 1, .10). Покажете графично с помощта на командатаGraphics Create Contour Plotстационарното разпределение на температурата в плочата.