Файлове със свободен индекс или файлове с последователен индекс
Нека се опитаме да подобрим начина, по който се съхранява файлът: ще го съхраним в подредена форма и ще приложим алгоритъм за двоично търсене за достъп до произволен запис. Тогава времето за достъп до произволен запис ще бъде значително по-малко. За нашия пример това би било:
T = log 2 KBO = log 2 12500 = 14 дискови достъпа.
А това е значително по-малко от 12 500 достъпа за произволно съхранение на файлови записи. Въпреки това поддържането на основния файл по редовен начин също е сложна операция.
Създаден е свободен индекс специално за подредени файлове. За тези файлове се използва принципът на вътрешно подреждане, за да се намали броят на съхранените индекси. Структурата на записа в индекса за такива файлове е следната:
Ключовата стойност на първия блоков запис
Блокирайте номер с този запис
В областта на индекса сега търсим желания блок по зададената стойност на първичния ключ. Тъй като всички записи са подредени, стойността на първия запис на блока ни позволява бързо да определим в кой блок се намира желаният запис. Всички други действия се извършват в основната зона. На фиг. Фигура 9.8 показва пример за това как да попълните основните и индексните области, ако първичният ключ е цели числа.
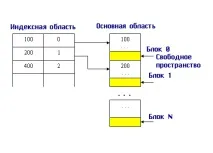
Ориз. 9.8. Пример за попълване на индекса и основната област при организиране на свободен индекс
Времето, необходимо за сортиране на големи файлове, е значително, но тъй като файловете се съхраняват сортирани от момента, в който са създадени, разходите за добавяне на нова информация ще бъдат много по-малко. Нека оценим времето за достъп до произволен запис за файлове с разхлабен индекс. Алгоритъмът за решаване на проблема е подобен.
LI = LK + 2 = 14 + 2 - 14 байта.
Тогава броят на индексните записи в един блок ще бъдее равно на:
KIZB = LB/LI = 1024/14 = 73 индексни записа в един блок.
Нека определим броя на индексните блокове, необходими за съхраняване на необходимите индексни записи:
KIB = KBO/KZIB = 12500/73 = 172 блока.
Тогава ще се определи времето за достъп по предходната формула:
Търсене T = log 2 KIB + 1 = log 2 172 + 1=8+1=9 дискови достъпа.
Виждаме, че при преминаване към свободен индекс времето за достъп намалява почти един път и половина. Следователно може да се признае, че организирането на свободен индекс дава печалба в скоростта на достъп.
Обмислете процедурите за добавяне и изтриване на нов запис с подобен индекс.
Тук механизмът за включване на нов запис е коренно различен от разгледания по-рано. Тук трябва незабавно да се въведе нов запис в необходимия блок на необходимото място, което се определя от зададения принцип на подреждане върху набора от стойности на първичен ключ. Следователно първо се търси необходимия блок от основната памет, в който трябва да се постави нов запис, след което този блок се чете, след което съдържанието на блока се коригира в RAM и отново се записва на диска на старото място. Тук, както и в първия случай, трябва да се зададе процентът на първоначално запълване на блока, но само по отношение на основната площ. В MS SQL сървъра този процент се нарича Full-factor и се използва при формиране на клъстерни индекси. Клъстерираните са просто индекси, в които оригиналните записи са физически подредени по стойностите на първичния ключ. Когато се направи нов запис, областта на индекса не се коригира.
Броят достъпи до диска при добавяне на нов запис е равен на броя достъпи, необходими за намиране на съответния блок плюс един достъп, койтое необходимо да пренесете променения блок на старото място.
T добавяния = log 2 N + 1 + 1 попадения.
Унищожаването на запис става чрез физическото му премахване от основната област, а индексната област обикновено не се актуализира, дори ако първият запис на блока е изтрит. Следователно броят на достъпите до диска при изтриване на запис е същият като при добавяне на нов запис.
Факт е, че във формулировката и изводите му е направена замяна, подобна на замяната в училищна шеговита загадка за находчивост, която пита: - Колко ябълки има на една бреза, ако има 5 на един клон, 10 на друг клон и т.н. В същото време вниманието на учениците умишлено се отклонява от основния факт, че ябълките по принцип не растат на бреза.
Експериментът на Майкелсън повдига въпроса за движението на етера спрямо интерферометър в покой в лабораторна система. Ако обаче търсим етера като основната материя, която изгражда цялата субстанция на интерферометъра, лабораторията и Земята като цяло, тогава, естествено, етерът също ще бъде неподвижен, тъй като земната субстанция е просто етер, устроен по определен начин и не може да се движи спрямо себе си.