Филтър за рекурсивна подвижна средна

Да, скъпи читателю, това също се случва и може да бъде вкусно и здравословно!
Както вероятно вече знаете, скъпи читателю, има два начина за изграждане на цифрови филтри. Това са рекурсивни филтри, те също са филтри с безкрайна импулсна характеристика (IIR), и напречни филтри, те също са филтри с крайна импулсна характеристика (FIR). Най-простият и най-широко използваният FIR филтър е "филтърът с подвижна средна стойност". Резултатът от филтрирането на такъв филтър е средноаритметичната стойност на последните N проби от входния сигнал.
Или разширено за N=4:
Функция на езика C, която реализира филтъра за подвижна средна:
Комплексното усилване на филтъра за пълзяща средна, нормализирано по отношение на честотата на дискретизация, се определя като преобразуването на Фурие на импулсния отговор:
Графиката на амплитудно-честотната характеристика (AFC), нормализирана по отношение на честотата на дискретизация, за различни дължини на филтъра (N=4;8;16), е показана на фигурата:
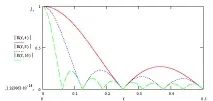
Съответно, графиката на фазово-честотната характеристика (PFC):
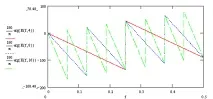
Този филтър е намерил широко приложение в обработката на сигнали, отчасти поради своята простота, но най-важното му свойство е линейна фазово-честотна характеристика и съответно постоянно забавяне на сигнала в цялата честотна лента. Този филтър трансформира амплитудния спектър на сигнала, без да засяга фазовия спектър, което го прави удобен за използване в системи за управление. Филтърът за пълзяща средна, поради своята линейна стъпкова характеристика, се използва широко при линейна интерполация, повторна дискретизация на сигнала и други подобни.
Основният недостатък на филтъра с подвижна средна е изчислителната сложност, пропорционална на дължинатафилтър N. За решаването на този проблем има рекурсивен филтър за пълзяща средна. Тоест филтър, който има същите характеристики като класическия филтър с подвижна средна, но реализиран по рекурсивна схема. Тези видове филтри са широко известни в тесни кръгове и се наричат: рекурсивни филтри с линейна фазова характеристика [Въведение в цифровото филтриране. Под. изд. Bogner R. M: 1976] или CIC филтри [DspLib]. Има научна школа на проф. Турулина И.И. [RSL], който се занимава с изследване на такива филтри.
Нека покажем как да изградим филтър с рекурсивна подвижна средна, използвайки примера на филтър с дължина N=4. Впоследствие няма да е трудно резултатите да се обобщят до произволна дължина на филтъра.
Както беше отбелязано по-горе, стойността на n-тата проба от сигнала на изхода на филтъра може да се определи като:
И стойността на предишния ((n-1)-ти) брой:
Изваждаме втория израз от първия израз, като резултат получаваме:
Лесно се вижда, че за произволна дължина на филтъра N, уравнението ще бъде написано в следната форма:
(1)
Въз основа на горното уравнение можем да напишем кода на филтъра на C, но първо ще проверим нашите изчисления. Нека намерим честотните характеристики на рекурсивния филтър с пълзяща средна, за който извършваме Z-преобразуване на уравнението на филтъра. Искам да напомня на скъпи читатели, че за извършване на Z-трансформация е необходимо да се заменят променливите (xn,yn) с техните Z-карти (X,Y), всяко намаляване на индекса на променливата с единица съответства на умножението на Z -1 .
Нека решим полученото уравнение по отношение на Y/X - усилване на филтъра
Нека преминем от Z-домейна към честотния домейн, като заменим с и получим комплексното усилване:
Нека изградим графика на модула на комплексния коефициент на пренос (AFC на филтъра), за различнистойности N=4,8,16:
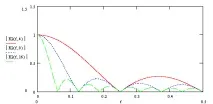
Както и аргументът на комплексното усилване (PFC на филтъра):
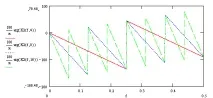
Както може да се види от горните графики, честотните характеристики на класическия филтър с пълзяща средна и рекурсивния филтър с пълзяща средна са абсолютно еднакви.
Да преминем към изпълнението на филтъра. Когато се прилага директно от филтърното уравнение (1) по отношение на целочислена аритметика, са възможни някои трудности. При извършване на операция деление на N в целочислена аритметика има загуба на значими битове, което води до нелинейно изкривяване на сигнала на изхода на филтъра. За да се разрешат тези трудности, е необходимо да се елиминира операцията за разделяне от уравнението на рекурентния филтър. За да направим това, умножаваме двете части на филтърното уравнение (1) по N.
В получения израз извършете заместването:
В резултат на това филтърното уравнение (1) се трансформира в система от уравнения:
На базата на системата от филтърни уравнения, ние пишем код, който реализира филтъра на езика C.
Заслужава да се отбележи, че любителите на „перфектния код“ могат да наложат ограничителни изисквания към дължината на филтъра N. С дължина на филтъра, равна на степени на две (2,4,8,16…), можете да замените операцията за деление (/) с аритметично отместване (>>), операцията за остатък (%) с побитова връзка (&).
Успех, скъпи читателю!
Hardcore conf в C++. Каним само професионалисти.