Газов модел на Ферми
В газовия модел на Ферми (FGM) нуклоните в ядрото се третират като нерелативистични фермиони, движещи се в потенциална яма. Основното предположение на модела е предположението, че линейните размери на кладенеца са много по-големи от дължините на вълните на нуклона:
| (6.1) |
Като първо приближение разгледайте решението на уравнението на Шрьодингер за частици в безкрайно дълбока правоъгълна потенциална яма. В този случай решението е y. Удобно е да търсите W под формата на продукт от три вълнови функции:
| () = (x)(y)(z) | (6.2) |
Решение при. Ш. вътре в ямата има проста форма:
| . (x) = a sin kxx + b cos kxx, (x) = 0 b = 0, (L) = 0 kxL = nx. | (6.3) |
Тук n е цяло число. Последните условия са следствие от "омрежването" на вълновата функция вътре и извън кладенеца. Общата енергия на една частица в кладенец е:
| (6.4) |
където N - цяло число - съответства на броя на запълнените състояния в кладенеца, а от (6.1) следва, че N >> 1.
 |
 |
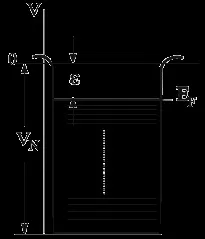
Максималната енергия на една частица в кладенеца се наричаенергия на Ферми(виж Фиг.6.1):
| . | (6,5) |
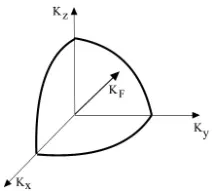
От уравнение (6.4) получаваме диференциала на броя на състоянията в кладенеца:
| dN = dnxdnydnz = L 3 dkxdkydkz / 3 = L 3 K 2 dKd/ 3 . | (6.6) |
Брой състояния на частици с енергия E
| . | (6,7) |
Обемът на ямката V е равен на обема на ядрото: V = (4/3)R 3 = (4/3)r0 3 A. Нека оценим нуклонната плътност на ядрото. Използвайки равенство (6.7), ние едновременно намираме връзката между импулса на Ферми и експериментално измерения параметър r0:
| . | (6,8) |
| ; . | (6,9) |
Получаваме, че нуклонната плътност на ядрото (6.8) е приблизително постоянна. Нуклонната плътност на ядрата е експериментално определена в експерименти върху разсейването на електрони с междинни енергии (E> 100 MeV) върху ядра. Тези експерименти бяха допълнени от експерименти върху разсейването на протони със същите енергии. Резултатът от тези експерименти беше представянето на разпределението на плътността на ядрената материя под формата на разпределението на Ферми:
| . | (6.10) |
При това се получи, че
| R r0A 1/3, r0 (1,2 - 1,3) fm. | (6.11) |
Нуклонната плътност на ядрата, според тези измервания, е близка до константа, за средни и тежки ядра почти не зависи от A и е приблизително От (6.9) получаваме стойността на импулса на Ферми:
| KF (1,25 - 1,35 (250 - 270) MeV/c. | (6.12) |
Следователно стойността на максималната кинетична енергия на частиците газ Ферми (енергия на Ферми) е. Трябва да се подчертае, че тази стойност при FGM не зависи от броя на нуклоните в ядрото.От това може да се получи и приблизителна стойност на дълбочината на ядрената потенциална яма. Тъй като средната енергия на отделяне на нуклон от ядро е около 8 MeV, дълбочината на потенциалната яма (виж фиг.6.1). Оценка на същата стойност може да се получи от други съображения, например от решаването на проблема с потенциала на деутрона. По този начин простият модел на газа на Ферми води до разумни оценки на дълбочината на потенциалния ядрен кладенец.
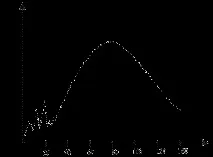 |
Фактът, че нуклоните на ядрото са в движение, е особено очевиден в реакциите на квазиеластично разсейване на електрони. Напречното сечение на този процес е широк максимум, разположен по-високо по енергия от областта на възбужданемногополюсни гигантски резонанси в ядрата (виж фиг.6.3). Ако разсейването на електрона се случи върху неподвижен нуклон, максимумът ще бъде при енергията, прехвърлена към ядрото, свързана с импулса q, прехвърлен към ядрото чрез проста нерелативистична връзка, където е прехвърленият импулс, M* е „ефективната“ маса на нуклона в ядрото. Но вместо тесен пик при тази енергия се наблюдава широк максимум на кривата на напречното сечение. Ширината му се дължи именно на Ферми движението на нуклоните в ядрото. Разсейването на електрона възниква - в ограничени случаи - както върху нуклон, движещ се към електрона, така и успоредно на импулса на електрона. Следователно измерването на ширините на пиковете на квазиеластичното разсейване е начин за независимо определяне на величината на импулса на Ферми. Таблица 1 изброява за няколко ядра стойностите на импулсите на Ферми, изчислени от данните за квазиеластичното разсейване на електрони.
Таблица 6.1. Ферми моменти за някои ядра.
| Ядро | KF, MeV |
| 7Li | 169 |
| 12C | 221 |
| 40 Ca | 251 |
| 58 Ni | 260 |
| 89 Y | 254 |
| 118 сн | 260 |
| 208Pb | 260 |
Газов модел на Ферми в астрофизиката
Експлозията на свръхнови води до появата или на неутронни звезди, или на черни дупки. Съдбата на свръхнова зависи преди всичко от масата. Енергията на Ферми на електроните в звезда е толкова голяма, че по време на експлозия в звезда протоните и електроните се превръщат в двойки неутрон-неутрино (обратен β-разпад: Процесът на обикновен β-разпад на неутрони е забранен от принципа на Паули за електроните (плътността на материята е толкова висока, че всички енергийни нива на електроните са заети, включително тези, които биха могли да бъдат заети от електрона, излъчен в този разпад).„Изгарянето“ на протоните води до изчезването на желязното ядро на звездата и превръщането му в неутронен ферми газ:
Броят на състоянията в потенциалната яма N ще бъде равен на броя на неутроните:
; 1 fm -1 = 200 MeV (с200 MeV fm = 1) kF(320 - 380) MeV/s; EF(50 - 70) MeV.
Гравитационното свиване на системата се съпротивлява от налягането на газа Ферми. Ако масата на ядрото на супернова е по-голяма от два пъти масата на Слънцето, гравитационните сили преодоляват налягането на газа Ферми и звездата се превръща в черна дупка. При по-ниски маси, кората на свръхновата се трансформира в неутронна звезда, в коятосилитена гравитационна компресия и налягането на неутронния газ са балансирани. Масата на неутронна звезда е приблизително Mnst 1.5MSun 3 · 10 30 kg, (изчислено от данните за доплеровото изместване), тогава Nn Mnst/mn 1.8. 10 57 - броят на неутроните в звездата. За да се получи условието за равновесие за звезда, е необходимо да се оцени средната кинетична енергия на движението на Ферми в звездата като функция от радиуса на звездата.
.
В неутронна звезда, импулсът на Ферми, радиусът на звездата е свързан с броя на неутроните N:
Rr0N 1/3; N = Mnst/mn 1.5MSun/mn = 1.8 10 57, следователно R13 km.
Оценка на радиуса на звезда може да се получи и от условието за равновесие, като се въведат в него зависимостите на средната кинетична енергия на движението на Ферми и средната енергия на гравитационно свиване от радиуса на звездата:
От условието за равновесие получаваме
(G = 6,7 . 10 -39 s. (GeV/c 2 ) -2 .)