Геодезическа задача
ГЕОДЕЗИЧЕСКА ЗАДАЧА, определяща задния азимут и координати на крайната точка от координатите на началната точка, азимута и дължината на линията, излизаща от тази точка (пряка геодезическа задача ), и определяне на дължината, както и предния и обратния азимут на линията от координатите на крайните й точки (обратна геодезическа задача ). Първа задача: според координатите x1 и y1, дължината на правата d и азимута α - координатите на края на правата x2 и y2 се изразяват по следния начин:
Втора задача: според координатите на краищата на правата x1, y1 и x2, y2 - дължината d и азимутът α се определят по формулите:
Много по-трудно е решението на геодезическата задача за прави и точки върху сфероид; тромавите формули на сфероидната тригонометрия са почти неприложими на практика. Трябва да се отбележи, че част от повърхността на земния сфероид може да се приеме за равнина и геодезическата задача може да бъде решена съгласно правилата на равнинната тригонометрия (виж по-горе); наистина, в кръг с радиус от около 7 km, линиите и ъглите на сфероида се различават толкова малко от линиите и ъглите, прехвърлени към равнината, допирателна в средата на сфероида, че тези разлики не се откриват дори при най-точните измервания; ако размерите на линиите надвишават тези размери, тогава трябва да се съобразите с геометричните характеристики на сфероида (елипсоид на въртене).
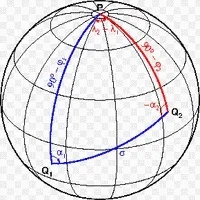
Известно е, че всички геодезически измервания на хоризонтални ъгли се извършват между вертикални нормални равнини. Това означава, че целевата равнина от А до В преминава през отвеса (нормална) в точка А и оставя следа върху повърхността на сфероида под формата на дъга от сфероида; ако точка B не е на същата географска ширина като A, тогава посоката на гравитационната линия в B ще бъде различна и зрителната равнина от A към B няма да съдържа отвеса B и, обратно, зрителната равнина от Bняма да съдържа отвеса в A и двете от тези наблюдения образуват две дъги върху повърхността на елипсоида, които не съвпадат една с друга, събирайки се в точки A и B и образувайки определен ъгъл. Най-голямата стойност на този ъгъл се изразява по формулата:
тук S е дължината на линията, а a е голямата полуос на земята (приблизително 6377 km). Стойността на този ъгъл обикновено е много малка и не надвишава 0,1" за линия от 100 km. Голямо удобство представлява замяната на нормалното сечение на сфероида с дъга от топка с радиус на кривина на първия вертикал; съотношението между тях се изразява с формулата:
където S е дъгата на сфероида, σ е дъгата на топка с радиус, равен на единица, ϱ2 е радиусът на кривината на първия вертикал, e е ексцентрицитетът на сфероида, ϕ е географската ширина и α е азимутът. Това означава, че разликата между дъгата на сфероида и дъгата на топката се изразява с малка стойност от пети ред, чиято най-голяма стойност ще бъде при ϕ = 0° и α = 0°; Тогава
Ако вземем голямата полуос a = 6377 km, e = 1:12, σ = 2π/360, т.е. дъга от 1 °, съответстваща на приблизително 112 km на земната повърхност, тогава
или 4 см, което дава относителна разлика на 112 км под формата на съотношение 1:3000000, което напълно отговаря на изискванията за най-точна геодезическа работа. Ако е желателно да не се надхвърля точността от 1:1000000, тогава трябва да се ограничат дъги от не повече от 192 km или, закръгляйки числото, 200 km. Практически е възможно радиусът на кривина на първия вертикал да се замени със средния радиус на кривина, което води до незначителни корекции в горните формули. Във всеки случай, линиите на земната сфероидна повърхност до 100 km, без да се засяга точността на случая, могат да се интерпретират като дъги на топка, т.е. сфероидните триъгълници могат да се интерпретират като сферични, като се решават според правилата на сферичната тригонометрия; по-нататъшното опростяване на изчисленията се основава на теоремата на Лежандър: акоза да разпределите ексцеса еднакво по ъглите на сферичен триъгълник, тогава такъв триъгълник може да бъде решен като плосък, тъй като изчисленото т.н. страните ще бъдат равни на страните на дадения сферичен триъгълник. Тук ексцесът се изчислява по формулата:
Методът на Бесел се основава на приемането на геодезическа линия и на прехвърлянето на изчисления от сфероид към топка с радиус a (a е голямата полуос на сфероида). Чрез сравняване на сферичен триъгълник със сфероиден, всички точки на сфероида се прехвърлят в сфера с радиус a, така че геодезичните линии се превръщат в дъги от окръжности, ширините на изображенията на точки върху сферата ще бъдат равни на намалените ширини върху сфероида, а азимутите на геодезичните линии запазват своите стойности. Остава да открием връзките: 1) между дължината на геодезическата линия S и дължината на съответната дъга върху топката δ и 2) между разликата в дължините на сфероида λ и съответния ъгъл w върху топката. Първото съотношение се изразява по формулата:
тук a е голямата полуос, e е ексцентричността, u е намалената географска ширина. Тези две диференциални уравнения служат като основни за решаване на геодезическата задача с помощта на метода на Бесел; те се решават чрез интегриране и разширяване на интеграндите в редица във възходящи степени на е. В тези серии човек може да се ограничи до различен брой членове, в зависимост от точността, с която се изискват изчисления във всеки отделен случай. Стойностите на спомагателните величини са дадени в специални таблици. В СССР се използва формулата на Шрайбер. През 1902 г. Военно-топографският отдел публикува "Таблици за изчисляване на ширините, дължините и азимутите на тригонометричните точки на елипсоида на Бесел" по формулите на Шрайбер. Съгласно формулите на Шрайбер разликата в ширината и дължината на линиите до 100 km може да се получи с точност до 0,001", а азимутите - с точност до 0,01", следователно, когатоКогато се използват тези формули, е необходимо да се прилагат седемцифрени логаритми и да се интерполира. Не може да не се отбележи съществуването на формули на Гаус, според които ширините и азимутите се получават чрез последователни приближения, а разликата в дължините се получава директно.
Източник: Martens. Техническа енциклопедия. Том 5 - 1929г