Геодезически мрежи, Инженерна геодезия
Има предвидени, високоетажни и пространствени мрежи. Планираните мрежи са тези, в които са определени планирани координати (плоски - x, y или геодезически - ширина B и дължина L) на точки. В мрежите за голяма надморска височина височините на точките се определят спрямо референтна повърхност, например повърхността на геоида (или по-скоро квазигеоида). В пространствените мрежи се определят пространствените координати на точките, например правоъгълни геоцентрични X, Y, Z или геодезични B, L, H.
6.1. Методи за изграждане на планирани мрежи
При изграждането на планирани мрежи за изходни точки служат отделни точки от мрежата - техните координати трябва да са известни. Координатите на останалите точки се определят чрез измервания, които ги свързват с оригиналните. Планираните геодезически мрежи се създават по следните методи.
Триангулацията е метод за определяне на планираното положение на геодезическите точки чрез изграждане на мрежа от триъгълници върху терена, в които се измерват ъгли, както и дължините на някои страни, наречени основни страни (фиг. 6.1).
Да приемем, че в триъгълника ABP са известни координатите на точките A (, ) и B (, ). Това позволява чрез решаване на обратната геодезическа задача да се определи дължината на страната и дирекционния ъгъл на посоката от точка А към точка В. Дължините на другите две страни на триъгълника ABP могат да се изчислят с помощта на синусовата теорема
; .
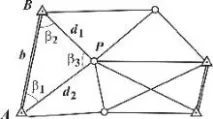
Ориз. 6.1. Диаграма на триангулационна мрежа
Продължавайки по този начин, изчислете дължините на всички страни на мрежата. Ако в допълнение към основата b са известни други бази (на фиг. 6.1 базите са показани с двойна линия), тогава дължините на страните на мрежата могат да бъдат изчислени с контрол.
Дирекционните ъгли на страните AP и BP на триъгълника ABP са равни
; .
Координатите на точката P се определят по формулите на директната геодезическа задача
; .
По същия начин изчислете координатите на всички други точки.
Трилатерацията е метод за определяне на планираното положение на геодезическите точки чрез изграждане на мрежа от триъгълници върху терена, в които се измерват дължините на техните страни.
Ако в триъгълника ABP (фиг. 6.1) основата b е известна и страните и са измерени, тогава въз основа на косинусовата теорема можете да изчислите ъглите на триъгълника;
;
;
. (6.1)
Ъглите на всички триъгълници също се изчисляват, а след това, както при триангулацията, координатите на всички точки.
Линейно-ъгловата мрежа се изгражда като правило като мрежа от триъгълници, в които се измерват ъгли и дължини на страните. Такива мрежи имат голям брой излишни измервания и следователно са много надеждни.
Полигонометрията е метод за определяне на планираното положение на геодезическите точки чрез полагане на прекъсната линия (полигонометричен ход) или система от взаимосвързани прекъснати линии (полигонометрични мрежи), в които се измерват ъглите на завъртане и дължините на страните.
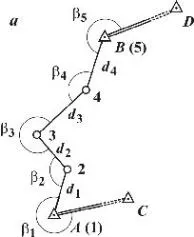
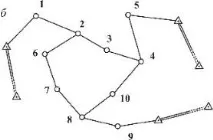
Ориз. 6.2. Полигонометрия: а - полигонометричен курс; b - система от ходове
Схемата на полигонометричния ход е показана на фиг. 6.2 a, където A и B са начални точки; CA и BD - начални направления, чиито дирекционни ъгли са известни; 1, 2, 3, 4, 5 - точки (върхове) на курса; - измерени хоризонтални ъгли - измерени дължини на страни (i = 1, 2, …).
На фиг. 6.2 b показва диаграма на система от полигонометрични ходове. Точки 2, 4, 8, където са свързани различни движения, се наричат възлови.
Сателитният метод за определяне на координатите на геодезически точки се основава на измервания от сателитни сигнали на навигационните системи ГЛОНАСС (България) и GPS (САЩ), извършвани от два (или повече) наземни приемника. Според резултатите от измерването разликите се определят с висока точност, , геоцентрични координати между точките. Ако координатите на една от точките са известни, тогава чрез добавяне на измерените разлики към тях се намират координатите на останалите точки. След това координатите се преобразуват в геодезични или равнинни правоъгълници.
Най-новите материали
Заключение (Почви)
При конструирането на курса е взета предвид необходимостта от използването му за различни хидротехнически специалности и специализации. Като основна част за студенти от всички хидротехнически специалности четенето на гл. 1-7. В гл. 8.
Идеи за решаване на проблеми от нелинейната механика на почвата
На съвременния етап от развитието на нелинейното направление на механиката на почвата се оформиха два основни подхода за решаване на практически проблеми за изчисляване на почвени основи и конструкции: нелинейно еластични и еластично-пластични (А. К. Бугров, С. С. Вялов.
Якост на почвата при сложно напрегнато състояние
За среди и материали с непрекъснатост са предложени много различни условия на якост. За оценка на якостта на почвите най-широко се използва условието на Мор-Кулон (2.38), което не съдържа междинното главно напрежение a2 и тях.
Основни закономерности на статичното деформиране на почвите
През последните 15,20 години, в резултат на многобройни експериментални изследвания, използващи горните тестови схеми, бяха получени обширни данни за поведението на почвите при сложно напрегнато състояние. Тъй като в момента в…
Еластично-пластична деформация на средата и натоварваща повърхност
Деформациите на еластопластичните материали, включително почвите, се състоят от еластични (обратими) и остатъчни (пластични). Да се съберат най-общи представи за поведението на почвитепри произволно натоварване е необходимо да се изучават отделно моделите ...
Описание на схемите и резултатите от изпитванията на почвата с помощта на инварианти на напрегнатото и деформираното състояние
При изучаването на почвите, както и на структурните материали, в теорията на пластичността е обичайно да се прави разлика между натоварване и разтоварване. Натоварването е процес, при който настъпва увеличаване на пластичните (остатъчни) деформации и процес, придружен от промяна (намаляване) ...
Инварианти на напрегнатото и деформирано състояние на почвената среда
Използването на инварианти на напрежение и деформация в механиката на почвата започва с появата и развитието на изследванията на почвата в устройства, които позволяват дву- и триосна деформация на образци при условия на сложно състояние на напрежение...
Относно коефициентите на стабилност и сравнение с експериментални резултати
Тъй като във всички проблеми, разгледани в тази глава, почвата се счита за най-напрегнато състояние, тогава всички резултати от изчисленията съответстват на случая, когато коефициентът на стабилност k3 = 1. За ...
Натиск на земята върху конструкции
Методите на теорията на граничното равновесие са особено ефективни при проблемите на определяне на натиска на почвата върху конструкции, по-специално подпорни стени. В този случай обикновено се приема дадено натоварване на повърхността на почвата, например нормалното налягане p (x) и ...
Носеща способност на основите
Най-типичният проблем на граничното равновесие на почвената среда е определянето на носещата способност на основата под действието на нормални или наклонени натоварвания. Например при вертикални натоварвания върху основата задачата се свежда до...
Процесът на отделяне на конструкциите от основите
Задача за оценка на състояниетоотделяне и определяне на силата, необходима за това, се случва при повдигане на плавателни съдове, изчисляване на силата на задържане на „мъртви“ котви, отстраняване на офшорни опори за гравитационно сондиране от земята по време на тяхното пренареждане и ...
Решения на задачи за равнинна и пространствена консолидация и техните приложения
Има много ограничен брой решения за плоски и още повече пространствени проблеми на консолидацията под формата на прости зависимости, таблици или графики. Има решения за случая на прилагане на концентрирана сила върху повърхността на двуфазна почва (B…