Геометрия. Урок 5
Съдържание на страницата:
- Дефиниция на кръг
- Сегменти в кръг
Кръг – геометрично място на точки, равноотдалечени от дадената точка.
Тази точка се наричацентър на окръжността.
Сегменти в кръг
Радиус на окръжността R е сегмент, свързващ центъра на окръжността с точка от окръжността.
Хорда a е отсечка, свързваща две точки от окръжността.
Диаметър d е хорда, минаваща през центъра на окръжността, равна е на два радиуса на окръжността (d = 2 R).
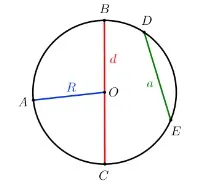
O A - радиус, D E - хорда, B C - диаметър.
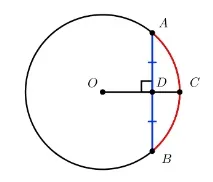
Теорема 1:Радиус, перпендикулярен на хорда, разполовява тази хорда и дъгата, към която се простира.
Допирателна към окръжността – права линия, която има една обща точка с окръжността.
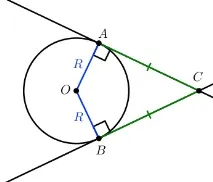
От една точка извън окръжността могат да се проведат две допирателни към дадената окръжност.
Теорема 2:Сегментите на допирателните, прекарани от една точка, са равни на ( A C = B C ).
Теорема 3:Допирателната е перпендикулярна на радиуса, прекаран към точката на контакт.
Дъга в кръг
Частта от окръжност, затворена между две точки, се наричаокръжна дъга.
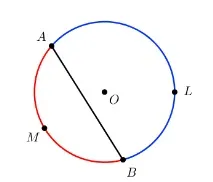
Например, хордата A B изважда две дъги: ∪ A M B и ∪ A L B .
Теорема 4:Равните хорди обхващат равни дъги.
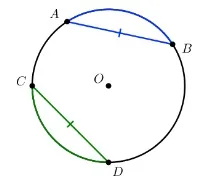
Ако A B = C D, тогава ∪ A B = ∪ C D
Ъгли в кръг
В кръга има два вида ъгли: централен и вписан.
Централен ъгъл – ъгъл, чийто връх е в центъра на окръжността.
∠ A O B е централен.
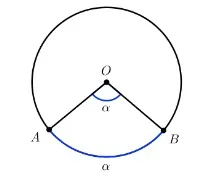
Централният ъгъл е равен на градусната мярка на дъгата, върху която лежи. ∪ A B = ∠ A O B = α
Ако начертаете диаметър, той ще раздели кръга на два полукръга. Градусната мярка на всеки полукръг ще бъде равна на градусната мярка на разширения ъгъл, който лежи върху него.
Градусът на целия кръг е 360°.
Вписан ъгъл – ъгъл, чийто връх лежи върху окръжността и чиито страни пресичат окръжността.
∠ A C B е вписано.
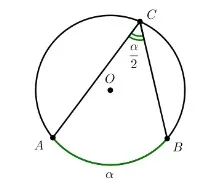
Вписаният ъгъл е равен на половината градусна мярка на дъгата, върху която лежи. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:Вписаните ъгли върху една и съща дъга са равни на.
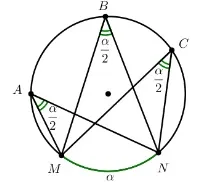
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:Вписаният ъгъл върху полукръга (диаметър) е 90 ° .
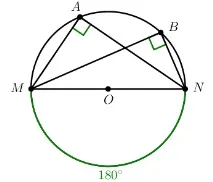
∠ M A N = ∠ M B N = ∪ M N 2 = 180° 2 = 90°
Обиколка, дължина на дъгата
Научихме как се измерва градусната мярка на дъга от окръжност (равна е на градусната мярка на централния ъгъл, който лежи върху нея) и цялата окръжност (градусната мярка на окръжност е 360 °). Сега нека поговорим за това каква е дължината на дъга в окръжност. Дължината на дъгата е стойността, която бихме получили, ако измерим дъгата с шивашки сантиметър. Да разгледаме две окръжности с различни радиуси, във всяка от които е построен централен ъгъл, равен на α.
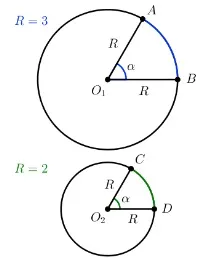
Градусната мярка на дъгата ∪ A B е равна на градусната мярка на дъгата ∪ C D и е равна на α .
Но с просто око можете да видите, че дължините на дъгите са различни. Ако градусната мярка на дъга от окръжност зависи само от стойността на централния ъгъл, който лежи върху нея, тогава дължината на дъгата от окръжност също зависи от радиуса на самата окръжност.
Обиколка се намира по формулата:
Дължината на дъгата на окръжност, върху която се опира централния ъгъл α, е равна на:
l α = π R 180 ∘ ⋅ α
Площ на кръг и неговите части
Сега нека поговорим за площта на кръга, площта на сектора и площта на сегмента.
Кръг — част от пространството, което е вътре в кръга.
С други думи,кръгът е границата, а кръгът е това, което е вътре.
Примери за кръг в реалния живот: колело на велосипед, обръч, пръстен.
Примери за кръг в реалния живот: пица, капак на шахта, плоска чиния.
Площта на кръг се намира по формулата: S = π R 2
Сектор е част от окръжност, ограничена от дъга и два радиуса, свързващи краищата на дъгата с центъра на окръжността.
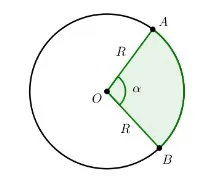
Примери за сектор в реалния живот: парче пица, вентилатор.
Площта на кръговия сектор, ограничен от централния ъгъл α, се намира по формулата: S α = π R 2 360 ° ⋅ α
Сегмент е част от окръжност, ограничена от дъга и хорда, която обхваща тази дъга.
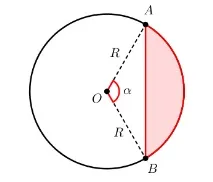
Примери за сектор в реалния живот: лимонов мармалад, лък за стрелба.
За да намерите площта на даден сегмент, първо трябва да изчислите площта на кръговия сектор, който съдържа този сегмент, и след това да извадите площта на триъгълника, образуван от централния ъгъл и хордата.
S = π R 2 180 ° ⋅ α − 1 2 R 2 sin α
Синусова теорема
Ако окръжност е описана около произволен триъгълник, тогава нейният радиус може да се намери с помощта на синусовата теорема:
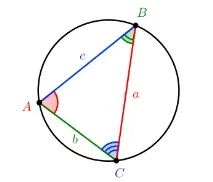
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достатъчно е да знаете една от страните на триъгълника и синуса на ъгъла срещу нея. От тези данни можете да намерите радиуса на описаната окръжност.
Примери за решениязадачи от OGE
Модул Геометрия: задачи свързани с окръжности.